Прочитайте внимательно текст и выполните задания 1–5.
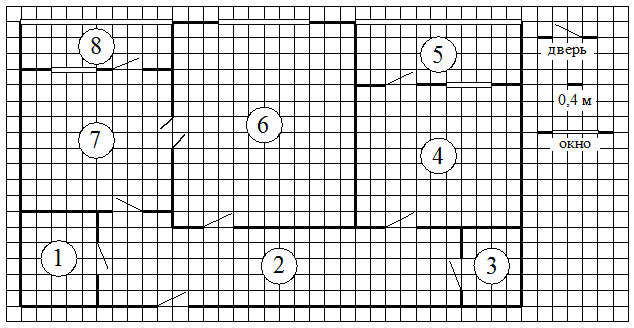
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом
с кладовой находится спальня, из которой можно пройти на одну
из застеклённых лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.
Анализ:
Подпишите все части комнаты перед тем, как приступите к выполнению задания. Вход в квартиру находится в коридоре, следовательно, он отмечен на плане цифрой 2, слева от входа в гостиную комнату отмечен санузел под цифрой 1, в противоположном конце под цифрой 3 отмечена кладовая. Из кладовой можно пройти в спальню, отмеченную цифрой 4, а из нее в лоджию, которая отмечена на плане цифрой 5. Гостиная, как самое большое помещение, отмечена цифрой 6, кухня — цифрой 7 и еще одна лоджия под цифрой 8.
1 — санузел, 2 — коридор, 3 — кладовая, 4 — спальня, 5 — лоджия в спальне, 6 — гостиная, 7 — кухня, 8 — лоджия в кухне.
Разбор задачи 1212 acmp.ru Укладка плитки. Решение на C++
Задание 1.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
Источник: gdzotvet.ru
Как решить задачу про плитки (ВПР 5 класс)?


Образование, обучение
Я не стал излагать условие задачи своими словами, а привожу прямо из учебника.
Так что условие задачи на картинке. В ответе на вопрос надо дать свое решение этой олимпиадной задачи.
Похожие страницы:
- Как решить задачу про самолет летящий из Владивостока в Москву ?
- Как решить задачу про цифры на электронных часах?
- Как решить задачу: В коробке лежат синие, красные и зелёные карандаши …?
- Вера и 1 кг конфет Кенгуру 2022 как решить задачу? какой набор дешевле?

Подписаться
3 комментариев
Межтекстовые Отзывы
Посмотреть все комментарии
1 год назад
Конечно эту задачу можно решить методом перебора. И вот тут компьютер реально пригодится. Но придется составлять программу.
Но можно применять логические приемы и решить задачу быстрее компьютера. Конечно такие задачи решают в школах. И к сожалению пути решения оставляют желать лучшего . Просто порой не совсем просто объясняют и в результате не каждый ребенок сможет понять даже готовое решение.
211128 1400 ОГЭ 01, часть1
А ведь с помощью элементарной формальной логики это можно сделать очень легко и все будет понятно любому ребенку , который учится в пятом классе. У меня такие проблемы стоят и я пытаюсь детям объяснить детям просто и тпк, чтобы они поняли.
И так перейдем к решению данной задачи.
Первое, что сразу бросается в глаза и позволяет сделать первый логический вывод.
Я просто процитирую часть условия.
то для квадратной площадки плиток не хватает. При укладывании по 8 плиток в ряд остается один неполный ряд
А получается, что у нас меньше 64 плиток, так как полный квадрат из 8 плиток в стороне это 64 плитки.
Так что дальше мы знаем из условия, что в ряду по восемь плиток не хватает, плиток, так как он неполный. И это значит, что из не больше семи.
Да необходимо добавить, Что плиток у нас больше 56. И это потому, что по восемь плиток мы выложили 7 рядов.
И получается, что у нас осталось плиток больше 56 и меньше 63, но включительно. Но последнее в условии задачи мы видим, что в последнем ряду по 8 плиток у нас больше одной плитки и меньше 7. А так как в ряду на 9 плиток их меньше на 6, чем в ряду по 8, то получается, что в ряду по восемь плиток у нас 7 плиток.
Вот и получается ответ 63 плитки.
К сожалению вынужден дать пояснение к своему ответу. Дело в том, что я копировал условие из учебника и там была допущена ошибка и пропущено число 6.
И вот как надо читать.
При укладывании по 8 пл. в ряд остается один неполный ряд, а при укладывании по 9- тоже остается неполный ряд, в котором на 6 пл. меньше, чем в неполном по 8 пл. Сколько всего плиток осталось
Так что еще раз приведу верное условие задачи.
После строительства осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки.
Если укладывать по 10 плиток, то для квадратной площадки плиток не хватает. При укладывании по 8 пл. в ряд остается один неполный ряд, а при укладывании по 9- тоже остается неполный ряд, в котором на 6 пл. меньше, чем в неполном по 8 пл. Сколько всего плиток осталось?
А здесь я приведу копию решения этой задачи из учебника.
Решение.
Поскольку при выкладывании по 8 и по 9 плиток в ряд прямоугольников не получается, а остаются неполные ряды, то количество плиток делится на 8 и на 9 с остатками.
Остаток от деления любого числа на 8 не может быть больше 7. По условию это число на 6 больше, чем остаток от деления на 9. Но остаток от деления на 9 тоже не равен нулю. Значит, остаток от деления на 8 может быть равен только 7. А остаток от деления на 9 равен 1.
Общее количество плиток меньше 100, иначе их хватило бы на квадратную площадку со стороной в 10 плиток. Среди чисел меньше 100 надо найти такое, которое делится на 8 с остатком 7 и на 9 с остатком 1. Проверив все числа в пределах 100, делящиеся на 9 с остатком 1, получим ответ: 55 плиток.
Получается, что ответы мой и из учебника не совпадают. Но теперь я опять приведу строчку из условия задачи.
При укладывании по 8 пл. в ряд остается один неполный ряд
А вот эта фраза из условия задачи свидетельствует, что у нас было не менее 7 рядов по восемь плиток. А значит больше 56 плиток.
Так что получается, что верный ответ это 63 плитки.
Я конечно извиняюсь, но эта задача не дает покоя. И при дополнительной проверке получается, что фраза из условия противоречит возможности решить данную задачу. Так что опять приведу эту фразу.
При укладывании по 8 пл. в ряд остается один неполный ряд
На самом деле тут можно понимать, что есть и еще пустые ряды. и тогда эту задачу реально можно решать только методом перебора. И это ясно, так как ответ 63 плитки просто не удовлетворяет условию задачи. И вот еще копия решения данной задачи.
Задачка не из простых. Здесь нужно думать математически плюс логически, что не каждому дано. поэтому просто берем карандаш в руки и рисуем на листочки плитки в рядах: один прямоугольник будет строиться из рядов по 9 плиток, а другой по 8 в каждом. В итоге наблюдаем видимую разницу в прямоугольниках на одну плитку в каждом ряду. Путем увеличения рядов, растет и разница.
После шестого ряда образуется разница в 6 плиток. Следовательно в восьмиплиточном прямоугольнике в неполном ряду должно быть на 6 плиток больше, чем в девятиплиточном прямоугольнике, а это 1+6 — наблюдается в шестом ряду.
Следовательно получаем: 6*8=48 плюс остаток в 7 плиток, в итоге 55. Это же условие выполняется, если 9*6=54 плюс остаток в 1 плитку, в итоге тоже 55.
Данное число еще и меньше 100, что удовлетворяет условию, которое изложено в третьем предложении задачи.
Ответ: 55 плиток осталось у строителей.
Так что приходится согласится с решением методом перебора, но при цсловии не обращать внимание на то что , я привел в цитате из условия задачи.
Источник: voprosfen.com
Впр по математике 5 класс задача про плитки решение задачи
Впр по математике 5 класс задача про плитки решение задачи

В магазине куртки продавались по цене 8 000 руб. за одну куртку. Летом на эту цену стала действовать скидка в 20%. Сколько рублей составляет скидка?
Найдем скидку: рублей.
Мама получила премию 180 руб. На подарок дочери она потратила 1% этой премии. Сколько рублей стоит подарок?
Найдем 1% от 180 рублей: руб.
В палатку завезли 850 кг огурцов. Покупатель взял для соления 3% всех огурцов. Сколько килограммов огурцов было куплено?
Найдем 3% от 850 килограммов: килограммов было куплено.
На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров хлопка они не убрали за сутки?
Не убрали всего поля. Тогда получим: гектаров хлопка не убрали за сутки.
Впр по математике 5 класс задача про плитки решение задачи

Принтер печатает 72 страницы за 3 минуты. За какое время этот принтер напечатает 120 страниц?
В минуту принтер печатает 72 : 3 = 24 страницы.
Время печати 120 страниц: 120 : 24 = 5 минут.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
Стальной шарик объёмом 6 см 3 имеет массу 46,8 г. Какова масса шарика из той же стали, если его объём 2,5 см 3 ?
Вычислим, сколько весит 1 см 3 шарика: 46,8 : 6 = 7,8 г.
Шарик объемом 2,5 см 3 будет весить 7,8 · 2,5 = 19,5 г.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени?
Вычислим, сколько масла можно получить из одного кг хлопкового семени:
Найдем теперь, сколько масла получится из 7 кг хлопкового семени: кг.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку?
Если 5 бульдозеров расчистили площадку за 210 мин, то у одного бульдозера на это уйдет в 5 раз больше времени: 210 · 5 = 1050 мин.
Вычислим, сколько времени уйдет на расчистку у 7 бульдозеров: 1050 : 7 = 150 мин.
Допускается другая последовательность действий, обоснованно приводящая к верному ответу.
Задачу можно решить, составив пропорцию: где х — время, необходимое 7 бульдозерам, чтобы расчистить площадку. Таким образом: минут.
Как решить задачу про плитку за 5 класс?
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на участке рядом с домом. если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватает. при укладывании по 6 плиток в ряд остается один неполный ряд, а при укладывании по 5 — тоже остается неполный ряд, в котором на 4 плитки меньше, чем в неполном ряду при укладывании по 6. Сколько всего плиток осталось после строительства дома?
Правильным ответом на вопрос задачи по математике, будет число «11, 41, или 71». Да, действительно получается такой ответ, давайте разбираться вместе, так как задачка довольно-таки запутанная.
- Во-первых, из условия задачи мы поняли, что необходимо выкладывать по шесть плиток в ряд. Получаем следующее неравенство 6Х + 5 = 5У + 1. 6Х + 4 = 5У Ведь укладывая по десять плиток в ряд по квардатной плодадке, то плиток не будет хватать. Далее лучше используем все числа, которые дают в остатке пять при делении 100 на 6. Нам подходят 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 83, 89, 95.
- Во-вторых, Для того, чтобы выявить совпадения, теперь необходимо найти числа, которые дают в остатке один при делении 100 на 5. Сюда относим 6, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, 66, 71, 76, 81, 86, 91, 96. Как видим, найдено совпадение это число «41 и 71» — осталось плиток после строительства дома.
Если укладывая по 10 плиток в ряд, до квадратной площадки плиток не хватает, то значит всего осталось плиток меньше 100 штук.
значит при укладывании по 6 плиток в неполном ряду будет 5 плиток, а при укладывании по 5 плиток в неполном ряду будет только одна плитка, других вариантов нет.
Если при укладывании по 6 плиток в ряд получилось Х полных рядов, а при укладывании по 5 плиток в ряд — У полных рядов, то можно составить равенство
Такое возможно при Х заканчивающимся на 1 или 6
Пусть F — это плитки по 5 штук в ряд, а W — плитки по 6 штук в ряд.
При укладывании плиток F в неполном ряду будет на 4 плитки меньше, чем в неполном ряду при укладывании W. Другими словами, при укладывании W в неполном ряду будет на 4 плитки больше, чем в неполном ряду при укладывании F.
Но в неполном ряду W может быть не более 5 плиток, а в неполном ряду F должна быть как минимум одна плитка.
Следовательно в неполном ряду W будет минимум может быть 1+4=5 плиток. А поскольку больше плиток в неполном ряду быть не может, то их количество равно 5.
Тогда в неполном ряду F на 4 плитки меньше, а 5-4=1.
Пусть количество полных рядов W будет х, а количество полных рядов W — это у.
Поскольку «х» — это целое число, то «у» должно заканчиваться на 1 или 6, в ином случае получается дробь.
1) Из того, что «. если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватает..», следует, что плиток менее 100.
2) Из того, что «. при укладывании по 5 плиток остается неполный ряд» следует, что в э
том варианте остаётся от 1 до 4 плиток.
3) Из того, что «. при укладывании по 5 — остается неполный ряд, в котором на 4 плитки меньше, чем в неполном ряду при укладывании по 6. » с учётом пункта 2, следует, что при укладывании по 6 плиток, должно оставаться от (1+4) до (4+4), т.е. от 5 до 8 плиток. Но существует единственное число, которое больше 4, и меньше 6, и это число — 5.
Значит при раскладывании по 6 плиток, остаётся 5 лишних, а при раскладывании по 5 плиток — 1 лишняя.
Пусть при раскладывании по 6 плиток в ряд, получается х рядов, а при раскладывании по 5 плиток в ряд у рядов. Тогда 6х+5=5у+1, 6х+4=5у, у=1,2х+0,8. Поскольку у — целое число, то произведение 1,2*у должно быть дробным числом, заканчивающимся на . 2.
х=6, у=1,2*6+0,8=8, количество плиток 41.
х=11, у=1,2*11+0,8=14, количество плиток 71,
х=16, у=1,2*16+0,8=20, количество плиток равно 101. Этот вариант не подходит, так как количество плиток меньше 100.
Но, просматривая варианты, можно для общности добавить ещё 1 вариант: х=1, у=2, количество плиток 11.
Конечно, при раскладывании 11 плиток по 6 плиток в ряд, получится всего лишь один ряд, но формально этот вариант тоже является решением.
Итак, плиток могло остаться либо 11, либо 41, либо 71.
Задания № 14 для подготовки к ВПР по математике 5 классе

Подборка заданий № 14 ВПР по математике 5 класс могут быть использованы как на уроке, так и во внеурочной деятельности.
Просмотр содержимого документа
«Задания № 14 для подготовки к ВПР по математике 5 классе»
Задания 14. Задачи повышенной трудности
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на участке рядом с домом. Если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватает. При укладывании по 8 плиток в ряд остается один неполный ряд, а при укладывании по 9 — тоже остается неполный ряд, в котором на 6 плиток меньше, чем в неполном ряду при укладывании по 8. Сколько всего плиток осталось после строительства дома?
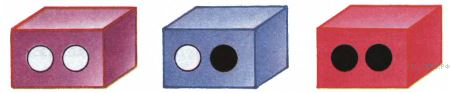
В одной коробке лежат два белых шара, в другой — два черных, в третьей — один белый и один черный. На каждой коробке имеется рисунок, но он неправильно указывает содержимое коробки. Из какой коробки, не глядя, надо вынуть шар, чтобы можно было определить содержимое каждой коробки?
На карточках написана двузначные числа. Сколько карточек нужно взять не глядя, чтобы по крайней мере одно из чисел делилось на 2 или на 7?
Два охотника отправились одновременно навстречу друг другу из двух деревень, расстояние между которыми 18 км. Первый шёл со скоростью 5 км/ч, а второй — 4 км/ч. Первый охотник взял с собой собаку, которая бежала со скоростью 8 км/ч. Собака сразу же побежала навстречу второму охотнику, встретила его, повернула и с той же скоростью побежала навстречу своему хозяину.
Встретила его, повернула и побежала навстречу второму охотнику и т. д. Так она бегала от одного охотника к другому, пока те не встретились. Сколько километров пробежала собака?
Женя за весну похудел на 20%, потом поправился за лето на 30%, за осень опять похудел на 20% и за зиму прибавил в весе на 10%. Остался ли за этот год его вес прежним? Уменьшился или увеличился?
Вася знает четыре числа, сумма которых равна 99. Если первое число увеличить на 2, второе уменьшить на 2, третье умножить на 2, а четвёртое разделить на 2, то каждый раз получается одно и то же число. Найдите эти четыре числа.
Возьмём любое четырёхзначное число, в котором есть различные цифры. Напишем его цифры в порядке убывания, а затем в порядке возрастания и вычтем из первого второе. (Если полученное при вычитании число не четырёхзначное, припишем спереди нули). С этим числом поступим так же. Продолжим этот процесс. Не позднее чем на 7-м шаге получим некоторое число, которое потом будет повторяться.
Найдите это число.
Из некоторого числа вычли сумму его цифр, из полученного числа вычли сумму его цифр и т. д. После одиннадцатого вычитания впервые получили 0. Каким могло быть первое число?
Имеется 9 листов бумаги. Некоторые из них разорвали на 3 или 5 частей. Некоторое из образовавшихся частей разорвали на 3 или 5 частей и так несколько раз. Можно ли после нескольких таких операций получить 100 частей?
В классе 25 учащихся. Из них 20 занимаются английским языком, 17 увлекаются плаванием, 14 посещают математический кружок. Докажите, что в классе найдётся хотя бы один ученик, который занимается английским языком, увлекается плаванием и посещает математический кружок.
Саша заметил, что когда он ехал в школу на автобусе, а возвращался на троллейбусе, то на весь путь было затрачено 35 мин. Когда же он туда и обратно ехал на автобусе, затратил 40 мин. Сколько времени потратит Саша на путь в школу и обратно, если будет ехать на троллейбусе?
В шести коробках лежат копейки. В первой — 1, во второй — 2, в третьей — 3 и т. д., в шестой — 6. За один ход разрешается в любые две коробки добавить по 1 копейке. Можно ли за несколько ходов уравнять количество копеек в коробках?
Два путешественника добирались из пункта А в пункт В. Первый путешественник сначала прошёл половину пути пешком, а затем вторую половину пути проехал на автобусе. Второй путешественник тоже шёл сначала пешком с такой же скоростью, как и первый путешественник, а затем тоже ехал на автобусе с такой же скоростью, как и первый путешественник. При этом оказалось, что второй путешественник шёл пешком столько же времени, сколько ехал на автобусе. Какой путешественник добрался из А в В за меньшее время?
Ночью к мосту через речку подошла семья: мальчик, мама, папа и бабушка. Мост выдерживает только двоих. Двигаться они могут со скоростью того, кто идёт медленнее, и при этом у них обязательно должен быть фонарик. За какое наименьшее время семья сможет переправиться на противоположный берег, если в одиночку для перехода через мост требуется: мальчику — 2 минуты, папе — 1 минута, маме — 5 минут, бабушке — 10 минут, а фонарик у них только один? (Нельзя светить издали, носить друг друга на руках, перебрасывать фонарик через мост).
Мотоциклист проезжает путь от деревни до станции за 0,3 ч. Он выехал из деревни, когда велосипедист, следующий по тому же маршруту со скоростью 15 км/ч, уже отъехал на расстояние 9 км. На станцию велосипедист и мотоциклист прибыли одновременно. На каком расстоянии от велосипедиста был мотоциклист через 10 мин после своего выезда?
В трех пассажирских поездах различное число мест: 236, 295, 472. Сколько вагонов в каждом поезде и сколько мест в каждом вагоне, если во всех вагонах число мест одинаковое?
К двузначному числу прибавили 5, и сумма оказалась кратной 5. Когда от него отняли 3, то разность оказалась кратной 3. Когда его поделили на 2, то оказалось, что и частное делится на 2. Найдите это число.
Сколько одинаковых изделий помещается в одной коробке, если в 13 коробках их меньше 118, а в 20 коробках больше 179?
Аквариум, имеющий форму прямоугольного параллелепипеда, изготовлен из пяти одинаковых кусков стекла, общей площадью 12 500 см 2 . Сколько литров воды потребуется для заполнения доверху трех таких же аквариумов?
Известно, что площадь Африки меньше площади Евразии, но больше площади Северной Америки. Площадь Южной Америки больше площади Антарктиды, но меньше площади Северной Америки. Антарктида по площади больше Австралии. Как называется материк с наибольшей площадью?
Три математика ехали в разных вагонах одного и того же поезда. Подъезжая к станции, они начали подсчитывать скамейки на привокзальном перроне. У них получилось 7, 12 и 15 скамеек. Отъезжая от станции, математики стали заново подсчитывать количество скамеек, причём один насчитал скамеек в три раза больше, чем другой. Сколько скамеек насчитал третий?
Несколько пятиклассников и шестиклассников обменялись рукопожатиями. При этом каждый пятиклассник пожал руку шести шестиклассникам, а каждый шестиклассник — пяти пятиклассникам. Кого было больше — пятиклассников или шестиклассников?
Математик Нуликов купил 20 одинаковых карандашей и несколько ластиков. Стоимость каждого ластика 15 р., а стоимость карандаша он забыл, помнит только, что она выражается целым числом рублей. Сможет ли Нуликов расплатиться за покупку без сдачи только пятирублёвыми монетами?
Было 7 листов бумаги. Некоторые из них разрезали на 7 частей, потом некоторые ещё разрезали на 7 частей, и такие действия повторили несколько раз. Могло ли в результате получиться 1 000 листов бумаги?
В одной группе 36 девочек, а в другой — 24 мальчика. Их надо разделить на равные команды, каждая из которых состоит или только из мальчиков, или только из девочек. Какое наибольшее число детей может быть в каждой команде? Сколько команд получится?
Из двух сцепленных шестерёнок одна имеет 16 зубцов, а другая — 28. До начала вращения шестерёнок соприкасающиеся зубцы пометили мелом. Через какое наименьшее число оборотов каждой шестерёнки метки совпадут?
Через остановку проходят автобусы, идущие по трём маршрутам. Один из них подходит к остановке через каждые 3 мин, другой — через каждые 6 мин, третий — через каждые 10 мин. В 8 ч 45 мин к остановке одновременно подошли все три автобуса. В какое ближайшее время там снова окажутся три автобуса?
Купец купил 110 фунтов табака. Пятьдесят фунтов оказались подмоченными, и купец продал их на 2 р. дешевле за 1 фунт, чем заплатил сам. Остальной табак он продал на 3 р. дороже за 1 фунт, чем заплатил сам. Подсчитайте прибыль купца.
На выставке-продаже до обеда было продано 15 картин, что составило  выставленных для продажи картин, а после обеда продали
выставленных для продажи картин, а после обеда продали  остатка. Оставшиеся на выставке картины распределили поровну между тремя магазинами. Сколько картин получил каждый магазин?
остатка. Оставшиеся на выставке картины распределили поровну между тремя магазинами. Сколько картин получил каждый магазин?
Орехи надо разложить в три пакета так, чтобы в одном пакете оказалось орехов в два с половиной раза меньше, чем в другом, но в два раза больше, чем в третьем. Сколько орехов надо положить в каждый пакет, если всего имеется 80 орехов?
Сева задумал натуральное число. Он умножил это число на 3, затем прибавил задуманное число, а к результату прибавил 17. В итоге у него получилось число 752. Докажите, что Сева ошибся в подсчётах.
Серёжа задумал натуральное число. Он умножил это число на 5, затем прибавил задуманное число, а из результата вычел 13. В итоге у него получилось число 544. Докажите, что Серёжа ошибся в подсчётах.
Источник: arxipedia.ru
