
При ремонте помещений часто возникает вопрос о количестве плиток, необходимых для покрытия определенной площади. Изучив эту статью, вы сможете узнать, сколько плиток вмещается на 1 квадратный метр, а также как правильно рассчитать их количество, используя специализированный расчетный метод.
Перед тем, как приступить к расчетам, необходимо учитывать размер плитки. Обычно плитки могут быть прямоугольной, квадратной или шестиугольной формы. Важно также учесть швы между плитками, которые необходимы для укладки. Стандартный шов составляет около 2-3 мм. При расчете учтите, что размеры плиток обычно указаны в сантиметрах.
Переведите размеры в метры, чтобы упростить расчеты.
Пример: если размер плитки составляет 30×30 см, переведем эти размеры в метры, чтобы получить 0.3×0.3 м. Теперь мы знаем, что площадь одной плитки равна 0.09 квадратного метра (0.3 м x 0.3 м = 0.09 м2).
Теперь разберемся с математикой. Для расчета количества плиток в 1 квадратном метре нужно разделить площадь одной плитки на площадь одного квадратного метра:
Площадь квадрата. Как найти площадь квадрата?
Количество плиток = площадь одного квадратного метра / площадь одной плитки
Продолжим пример. У нас есть площадь одной плитки равная 0.09 квадратного метра. Рассчитаем количество плиток:
Количество плиток = 1 / 0.09 = 11.11
Таким образом, в 1 квадратном метре поместится примерно 11.11 плиток.
Как рассчитать количество плиток в 1 квадратном метре
Для правильного расчета количества плиток, необходимых для покрытия 1 квадратного метра, необходимо учесть несколько факторов:
- Размер плитки. Обычно размер плитки указывается в сантиметрах. Например, 10×10 см.
- Способ укладки. Возможны различные способы укладки плитки, которые могут потребовать дополнительных расчетов.
- Дополнительные затраты на обрезку. В процессе укладки плитки могут возникать ситуации, когда плитку необходимо обрезать под нужный размер.
Для простоты расчета можно использовать следующую формулу:
Количество плиток = (Площадь помещения) / (Площадь одной плитки)
Для примера, рассмотрим помещение площадью 6 м², где используются плитки размером 10×10 см:
Площадь одной плитки = (10 см) * (10 см) / (100 см²/м²) = 0,01 м²
Количество плиток = (6 м²) / (0,01 м²) = 600 плиток
В данном примере не учитывались дополнительные затраты на обрезку плиток. Если такие затраты предполагаются, рекомендуется приобрести некоторое количество плиток в запасе.
| 10×10 | 0,01 | 100 |
| 15×15 | 0,0225 | 44 |
| 20×20 | 0,04 | 25 |
В зависимости от размера плитки, количество плиток на 1 квадратный метр будет различаться. Таблица приведена для информационных целей и может варьироваться в зависимости от точного размера плитки и ее укладки.
КАК РАССЧИТАТЬ | ПЛОЩАДЬ СТЕН❓
Расчет количества плиток в 1 квадратном метре поможет определить необходимое количество материала для покрытия пола, стен или других поверхностей плиткой.
Какие параметры плитки влияют на расчет
Форма плитки: Также форма плитки может влиять на расчет. Если плитка имеет нестандартную форму, то ее укладка может требовать большего количества резки и, соответственно, большего количества плитки.
Процент отходов: При расчете количества плитки необходимо учитывать процент отходов. Он зависит от сложности укладки и качества работы исполнителя. Обычно рекомендуется добавлять 10-15% к расчетному количеству плитки.
Толщина плитки: Толщина плитки также может влиять на расчет. Если плитка имеет большую толщину, то при укладке возможно потребуется больше материала.
Узор и направление укладки: Если плитка имеет узор или требуется особое направление укладки, то это также может повлиять на расчет количества плитки. В некоторых случаях требуется приобретать дополнительную плитку для согласования узора.
Учет вырезов и дверных проемов: Когда плитка укладывается на пол, необходимо учитывать вырезы под дверные проемы или другие конструктивные элементы. Для таких случаев может потребоваться дополнительная плитка.
Применение клея: При расчете количества плитки следует учесть также необходимость использования клея. Количество клея зависит от размеров плитки и способа укладки, поэтому при расчете его также необходимо учесть.
Формула расчета плиток на основе их размеров
Когда вы покупаете плитку для облицовки пола или стен, важно знать, сколько плиток вам понадобится для покрытия нужной площади. Для расчета количества плиток используется специальная формула, которая основывается на размерах плитки и площади поверхности.
Формула для расчета количества плиток имеет следующий вид:
Количество плиток = Площадь поверхности / (Ширина плитки * Длина плитки)
- Площадь поверхности — площадь пола или стены, которую вы планируете покрыть плитками;
- Ширина плитки — горизонтальный размер плитки (обычно измеряется в сантиметрах);
- Длина плитки — вертикальный размер плитки (также измеряется в сантиметрах).
Например, у вас есть площадь пола 10 квадратных метров, а размеры плитки составляют 20 см в ширину и 30 см в длину. Для расчета количества плиток применяем формулу:
| 10 м² | 20 см | 30 см | ? |
Подставим значения в формулу:
Количество плиток = 10 м² / (20 см * 30 см)
Для удобства расчета необходимо привести все размеры к одной единице измерения. В данном случае, можно привести размер плитки к метрам:
Количество плиток = 10 м² / (0.2 м * 0.3 м)
Далее производим вычисления:
Количество плиток = 10 м² / 0.06 м² = 166.67
Итак, вам понадобится около 166.67 плиток для покрытия площади в 10 квадратных метров с использованием плиток размером 20×30 см.
Учтите, что в реальности нужно покупать не только целые плитки, но и некоторое количество запасных плиток на случай повреждений или ошибок при укладке.
Как учесть швы между плитками в расчете
При расчете количества плиток, необходимых для покрытия определенной площади, необходимо учесть швы между плитками. Шов между плитками необходим для компенсации усадки плит и предотвращения трещин. Также шов позволяет создать более эстетичный внешний вид покрытия.
Чтобы учесть швы между плитками в расчете, необходимо знать ширину шва. Ширина шва обычно составляет от 2 до 10 мм в зависимости от размера плитки и требований дизайна. В среднем используется ширина шва 3-5 мм.
Для расчета количества плиток с учетом швов необходимо учесть не только площадь самой плитки, но и площадь шва. Для этого вычисляется площадь одной плитки с учетом шва и затем делится на площадь плитки без учета шва. Результатом будет количество плиток, необходимых для покрытия определенной площади с учетом швов.
Например, для плитки размером 30×30 см и швом шириной 3 мм:
Площадь плитки с учетом шва:
Ширина плитки + 2 * ширина шва = 30 см + 2 * 0.3 см = 30.6 см
Высота плитки + 2 * ширина шва = 30 см + 2 * 0.3 см = 30.6 см
Площадь плитки с учетом шва = 30.6 см * 30.6 см = 937.2 см²
Площадь плитки без учета шва:
Ширина плитки = 30 см
Высота плитки = 30 см
Площадь плитки без учета шва = 30 см * 30 см = 900 см²
Количество плиток с учетом шва:
Площадь покрытия / площадь плитки с учетом шва = 1000 м² / 937.2 см² ≈ 1.07 (округляем до ближайшего целого числа)
Таким образом, для покрытия площади 1000 м² понадобится примерно 2 плитки размером 30×30 см с учетом шва шириной 3 мм.
Пример расчета количества плиток в 1 квадратном метре
Для расчета количества плиток в 1 квадратном метре необходимо знать размеры плитки и ее форму. Рассмотрим пример.
- Предположим, что размер плитки составляет 10 см х 10 см.
- Для простоты расчета, переведем размеры плитки в метры, получим 0.1 м х 0.1 м.
- Теперь посчитаем площадь одной плитки: 0.1 м * 0.1 м = 0.01 кв. м.
Переходим к расчету количества плиток в 1 квадратном метре.
-
Разделим площадь одной плитки на площадь 1 квадратного метра:
1 кв. м / 0.01 кв. м = 100 плиток.
Приведенный выше пример демонстрирует, как можно расчитать количество плиток в 1 квадратном метре и может быть применен в различных ситуациях для получения нужного количества плиток при ремонте или строительстве.
Как варианты формы и размера плиток влияют на количество в 1 квадратном метре
При выборе плиток для покрытия пола или стен важно учесть не только их внешний вид, но и количество, которое потребуется для покрытия определенной площади. Количество плиток в 1 квадратном метре будет зависеть от их формы и размера.
Одна из самых распространенных форм плиток — это квадратная форма. Квадратные плитки обычно имеют стороны от 10 до 60 см. Чем больше размер плитки, тем меньше их количество в 1 квадратном метре. Например, если квадратная плитка имеет размер 10 см, то для покрытия 1 квадратного метра потребуется 100 плиток. Если же размер плитки 60 см, то потребуется всего около 3 плиток для покрытия той же площади.
Однако, помимо квадратных, существуют плитки других форм, например, прямоугольные. Прямоугольные плитки могут иметь разные пропорции, например, 1:2 или 1:3. В зависимости от пропорций прямоугольных плиток, их количество в 1 квадратном метре может варьироваться. Например, если прямоугольная плитка имеет пропорции 1:2 и размеры 15×30 см, то для покрытия 1 квадратного метра потребуется около 22 плиток.
Кроме того, форма плиток может быть и нестандартной, например, шестиугольной или пятиугольной. В таком случае, количество плиток в 1 квадратном метре будет зависеть от размеров и формы плиток. Нестандартные формы часто требуют особого подбора и расчета для оптимального использования и минимизации отрезков при монтаже.
При выборе плиток для покрытия площади необходимо учитывать не только их внешний вид, но и количество, которое потребуется для покрытия желаемой площади. Необходимо провести расчет, исходя из выбранной формы и размера плитки, чтобы избежать недостатка или излишка материала при монтаже.
Итак, при выборе плиток для покрытия 1 квадратного метра, важно учитывать их форму и размер. От этого будет зависеть количество плиток, необходимых для покрытия данной площади. Квадратные плитки с меньшим размером потребуют большего количества, в то время как плитки большего размера позволят сократить количество. При выборе прямоугольных или нестандартных плиток, также необходимо учитывать их размеры и пропорции для определения количества материала, необходимого для покрытия 1 квадратного метра.
Другие факторы, которые могут влиять на количество плиток в 1 квадратном метре
В дополнение к размеру плитки, есть также несколько других факторов, которые могут влиять на количество плиток, укладываемых в одном квадратном метре. Вот некоторые из них:
| Форма плитки | Плитки с нестандартной формой могут требовать дополнительной обрезки и неудобной укладки, что может увеличить количество отходов и снизить плотность укладки. Например, шестиугольные или шестиугольные плитки могут иметь больше пустого пространства между ними, по сравнению с квадратными или прямоугольными плитками. |
| Структура поверхности | Плитки с текстурированной или выпуклой поверхностью могут требовать больше пространства между ними для компенсации неровностей поверхности. Это может привести к меньшей плотности укладки и увеличению количества отходов. |
| Способ укладки | Некоторые способы укладки плитки, такие как диагональная укладка или использование декоративных элементов, могут требовать больше плиток и увеличить количество отходов. Также может потребоваться больше времени и навыков для правильной установки таких плиток. |
| Размер шва | Ширина шва между плитками может влиять на количество плиток, которые могут поместиться в одном квадратном метре. Более широкие швы требуют больше пространства и могут уменьшить плотность укладки. |
| Необходимость обрезки | При работе с пространствами, имеющими нестандартную или сложную форму, может потребоваться обрезка плиток. Большее количество отходов может увеличить общее количество требуемых плиток. |
| Рельефность поверхности укладки | Если поверхность, на которую вы укладываете плитку, неровная или имеет много выступов и впадин, может потребоваться больше плиток для создания равномерной поверхности. |
Учитывая эти дополнительные факторы, важно учесть не только размер плитки, но и ее форму, структуру поверхности, способ укладки и другие факторы при расчете количества плиток, необходимых для покрытия одного квадратного метра.
Источник: das1knitu.ru
План участка (хозяйственная задача)

Первые пять заданий ОГЭ 2020 по математике объединяет одна картинка, на которой изображен план участка. Под картинкой располагается текст, описывающий расположение объектов на этой картинке.
Для успешного выполнения этих заданий потребуется внимательность, умение логически мыслить, вычислять площадь прямоугольника, и применять теорему Пифагора.
Прочитайте внимательно текст и выполните задания 1-5.

На плане изображено домохозяйство по адресу: с. Авдеево,3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м. Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м×1м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.
К домохозяйству подведено электричество. Имеется магистральное газоснабжение.
Задание №1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Таблица соответствия объектов номерам на картинке.
По условию задачи справа от ворот находится баня (6), а слева гараж (7 – по условию). Ещё на участке есть сарай, жилой дом и теплица. На огороде (2 – по условию) стоит теплица (1), рядом с гаражом (7) стоит сарай (4). Яблоневые посадки (5 – по условию) находятся рядом с домом, следовательно дом (3).
Ответ: 3461
Задание №2. Тротуарная плитка продаётся в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?
Посмотрим на картинку. По условию задачи одна тротуарная плитка имеет размер 1м×1м и на картинке отмечена серым цветом. Нам нужно сосчитать количество серых плиток на рисунке. Площадку перед гаражом покрывают 4х16=64 плитки, дорожки застелены 26 плитками. Всего плиток 64+26=90 штук.
Чтобы понять, сколько упаковок нам нужно купить, разделим общее количество плиток на количество плиток в одной упаковке: 90/4=22,5. В магазине плитка продаётся целыми пачками, поэтому придется брать 23 упаковки, округление с избытком.
Ответ: 23
Задание №3. Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.
Сперва посчитаем, сколько тетрадных клеток занимает дом (3). Дом занимает 17 тетрадных клеток. Далее есть три пути решения:
Путь 1 (знаем сторону клетки): На рисунке показано, что сторона одной квадратной клетки составляет 2 м. Значит площадь одной квадратной клетки равна 2×2=4 кв. м. А площадь дома равна 4×17=68 кв. м.
Путь 2 (через площадь плитки): Если бы размер одной клетки не был нам дан, пришлось бы решать задачу другим способом. Одну тетрадную клетку можно застелить четырьмя серыми плитками. Площадь одной плитки составляет 1 кв. м., значит площадь одной тетрадной клетки составляет 4 кв. м. Площадь дома равна 4×17=68 кв. м.
Путь 3 (через площадь сарая): По условию задачи площадь гаража (7) равна 32 кв. м. Гараж занимает 8 тетрадных клеток, следовательно, площадь одной тетрадной клетки равна 32/8=4 кв. м. Тогда площадь дома равна 4×17=68 кв. м.
Все три пути решения привели нас к одному и тому же ответу, и это однозначно успех .
Ответ: 68
Задание №4. Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.
Посмотрим на картинку.
Проведём красным цветом кратчайший отрезок, соединяющий дом (3) и сарай (7). Этот орезок является гипотенузой в прямоугольном треугольнике с катемтами 3 и 4 клетки. Длина стороны одной клетки по условию 2м, значит один катет 6м, а другой 8м. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, значит:
x = ± 10 = [ − 10 не подходит 10 подходит
Ответ: 10
Задание №5. Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице. Обдумав оба варианта, хозяин решил установить газовое оборудование.
Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления?
Цены на оборудование и стоимость его установки.
Вычислим, сколько денег переплатил хозяин, установив газовое оборудование:
24000 – 20000 + 18280 – 15000 = 4000 + 3280 = 7280
Хозяин переплатил 7280 рублей, установив газовое оборудование. Вычислим, сколько экономит хозяин в час, используя газовое оборудование вместо электрического отопления:
5 , 6 ⋅ 3 , 8 – 1 , 2 ⋅ 5 , 6 = 5 , 6 ⋅ ( 3 , 8 – 1 , 2 ) = 5 , 6 ⋅ 2 , 6 = 14 , 56
Каждый час работы газового оборудования хозяин экономит 14,56 рубля. Пусть генератор работал непрерывно x часов. Тогда:
x ⋅ 14 , 56 = 7280
x = 7280 14 , 56 = 500
За 500 часов непрерывной работы экономия от использования газового оборудования покроет переплату за его установку.
Ответ: 500
Источник: epmat.ru
Как найти дискриминант квадратного уравнения? Онлайн-калькулятор
Самое главное в 8 классе — научиться применять формулы для решения квадратных уравнений. А дискриминант тут очень кстати! Давайте разбираться вместе, как решать задачки через дискриминант.
· Обновлено 11 сентября 2023
Онлайн-калькулятор для нахождения дискриминанта квадратного уравнения
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0.
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac.
Домашний лицей для 5–11 классов
Занятия где и когда удобно, 10+ кружков на выбор, никакого стресса с домашками и нудных родительских собраний

Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
- 5 + 8 = 12;
- 13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
- 2x 2 − x + 5 = 0
- a = 2, b = −1, c = 5
Такое уравнение можно решить с помощью формулы дискриминанта.
Выберите идеального репетитора по математике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения

Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
- Определим, чему равны коэффициенты a, b, c.
- Вычислим значение дискриминанта по формуле D = b2 − 4ac.
- Если дискриминант D < 0, то корней нет. Если D = 0, то есть один корень, равный −b/2a. Если D >0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.
Пример 2. Решить уравнение: x 2 — 6x + 9 = 0.
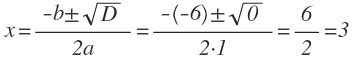
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.
- D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.
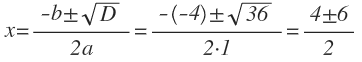
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.
- D > 0, значит уравнение имеет два корня:
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Источник: skysmart.ru