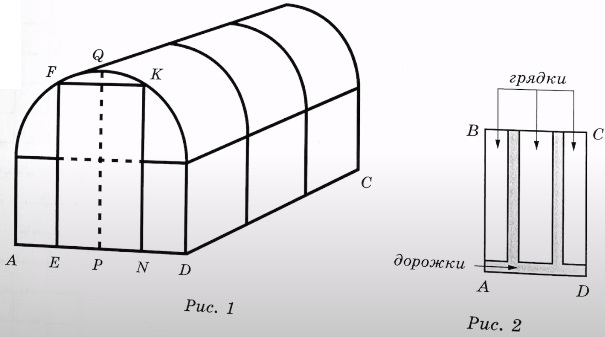
Юрий Борисович начал строить на дачном участке теплицу (рис. 1). Для этого он сделал прямоугольный фундамент длиной 6 м (DC на рис. 2) и шириной 2,4 м (AD на рис. 2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплён металлическими стойками.
Высота нижнего яруса теплицы в два раза меньше её ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы.
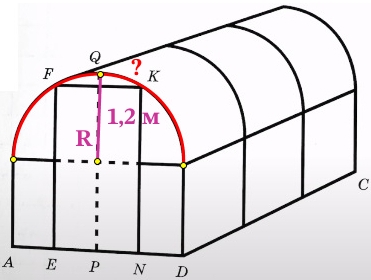
В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20×20 см.
Решаем ОГЭ 2023 математика Ященко вариант 1
Источник: ОГЭ Ященко 2023 (36 вар)
Задание 1
Найдите высоту теплицы PQ в метрах.
Решение:
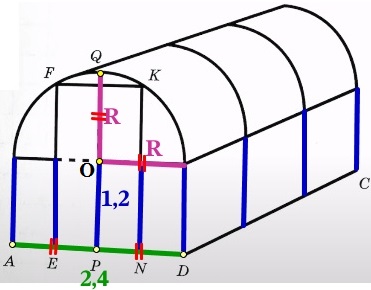
Высоту теплицы PQ можно найти следующим образом:
PQ = PO + OQ
РО – это высота нижнего яруса теплицы, который в два раза меньше её ширины AD:
PO = AD/2 = 2,4/2 = 1,2 м
OQ – это радиус полуокружности верхнего яруса теплицы, равный половине ширины теплицы AD (т.к. E, P и N делят отрезок AD на равные части):
R = OQ = PD = AD/2 = 2,4/2 = 1,2 м
Найдём высоту теплицы PQ:
PQ = PO + OQ = 1,2 + 1,2 = 2,4 м
Ответ: 2,4.
Задание 2
Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 6 штук?
Решение:
По условию ширина грядок равна 40 см . Длина нижней дорожки, равна ширине теплицы AD = 2,4 м = 240 см . Длины двух других дорожек равны длине теплицы СВ = 6 м = 600 см :
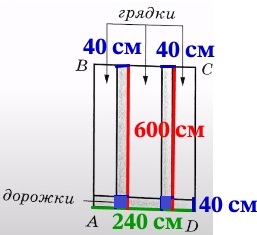
Найдём общую площадь всех трёх грядок:
40 · 240 + 40 · 600 + 40 · 600 = 40·(240 + 600 + 600) = 40·1440 = 57600 см 2
Дорожки пересекаются, площадь двух квадратов посчитали дважды, вычтем их:
57600 – 40 · 40 – 40 · 40 = 54400 см 2
Площадь одной тротуарной плитки равна 20х20 см:
20·20 = 400 см 2
Найдём сколько нужно купить:
54400/400 = 136 плиток
В одной упаковке 6 плиток, значит надо купить:
Понятный разбор ОГЭ по математике 2023 Ященко вариант 1. Часть 1. Теплицы | Умскул
Такое количество упаковок нам не продадут, значит надо брать минимум 23 упаковки.
Ответ: 23.
Задание 3
Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки. Ответ дайте в сантиметрах.
Решение:
Пусть ширина каждой из узких грядок равна х , тогда ширина центральной грядки 1,2х . Зная все расстояния, составим уравнение и найдём х:
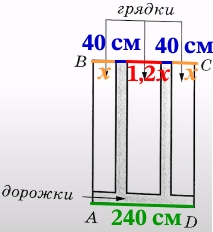
х + 40 + 1,2х + 40 + х = 240
3,2х + 80 = 240
3,2х = 240 – 80
3,2х = 160
х = 160/3,2 = 50 см
Найдём ширину центральной грядки:
1,2х = 1,2·50 = 60 см
Ответ: 60.
Задание 4
Найдите длину металлической дуги для верхнего яруса теплицы. Ответ дайте в метрах, округлив его в большую сторону с точностью до десятых.
Решение:
Длина металлической дуги, это половина длины окружности с радиусом равным 1,2 м . Найдём по формуле длину окружности:
С = 2πR = 2·3,14·1,2
Длина дуги в два раза меньше, округлим в большую сторону до десятых:
Ответ: 3,8.
Задание 5
Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.
Решение:
Высоту EF можно найти следующим образом:
EF = EV + VF
EV – это высота нижнего яруса теплицы он равен 1,2 м = 120 см .
Рассмотрим ΔFVO, он прямоугольный, в нём FO = 1,2 м = 120 см , как радиус дуги. VO = EP , как параллельные стороны прямоугольника, и равен 2,4/4 = 0,6 м = 60 см .
В прямоугольном ΔFVO, по теореме Пифагора, найдём VF:
FO 2 = VF 2 + VO 2
120 2 = VF 2 + 60 2
120 2 – 60 2 = VF 2
10800 = VF 2
VF = √10800
Найдём высоту EF, в сантиметрах с точностью до целого:
EF = EV + VE = 120 + sqrt = 120 + sqrt=120+sqrtcdot 3^cdot 10^>=120+2cdot 3cdot 10cdot sqrt=120+60cdot sqrtapprox 120+60cdot 1,73 approx 120+103,8approx 223,8approx 224: см
По ответам сборника, будет верный любой ответ в диапазоне 222 – 225 см.
Ответ: 224.
Источник: ege314.ru
Сколько нужно упаковок плитки для дорожек если в каждой упаковке 6 штук
Юрий Борисович начал строить на дачном участке теплицу (рис. 1). Для этого он сделал прямоугольный фундамент длиной 6 м (DC на рис. 2) и шириной 2,4 м (AD на рис. 2).
Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплён металлическими стойками. Высота нижнего яруса теплицы в два раза меньше её ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса.
Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником EFKN, где точки Р и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20 х 20 см.


Задание 1. Найдите высоту теплицы PQ в метрах.
Так как верхний ярус теплицы – полуокружность с диаметром длиной AD = 2,4 м, то радиус этой полуокружности составляет:
h = R = 2,4 : 2 = 1,2 м.
Высота нижнего яруса также в два раза меньше AD (по условию задания) и равна 2,4 : 2 = 1,2 м. Следовательно, высота теплицы:
Задание 2. Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 6 штук?
Сначала вычислим общую площадь дорожек. Ширина каждой составляет 40 см. Длина горизонтальной дорожки AD = 2,4 м = 240 см. Длины двух вертикальных:
AB – 40 см = 600 – 40 = 560 см
(мы здесь вычитаем ширину горизонтальной дорожки, чтобы дважды не учитывать площадь пересечений).
Таким образом, общая площадь дорожек, равна:
Площадь одной плитки
где — оператор округления до наибольшего целого.
Задание 3. Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки. Ответ дайте в сантиметрах.
Пусть x см – ширина узкой грядки. Тогда всю ширину AD = 2,4 м = 240 см можно записать в виде уравнения:
То есть, ширина узкой грядки равна 50 см, а широкой:
Задание 4. Найдите длину металлической дуги для верхнего яруса теплицы. Ответ дайте в метрах, округлив его в большую сторону с точностью до десятых.
Так как дуга представляет собой полуокружность с радиусом м, то ее длина, равна:
Округляем до десятых, имеем:
Задание 5. Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.
Точка P – центр отрезка AD, а точка N – четверть отрезка AD (по условию задания). Нужно найти высоту EF, которая складывается из высоты основания 1,2 м = 120 см и высоты h прямоугольного треугольника с гипотенузой R и вторым катетом ND = AD : 4 = 60 см.

Найдем высоту h по теореме Пифагора:
Таким образом, высота входа в теплицу примерно равна:
Источник: self-edu.ru
ОГЭ 2020 задания 1 — 5 (теплица)
Прочитайте внимательно текст и выполните залдания 1 — 5.
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент.
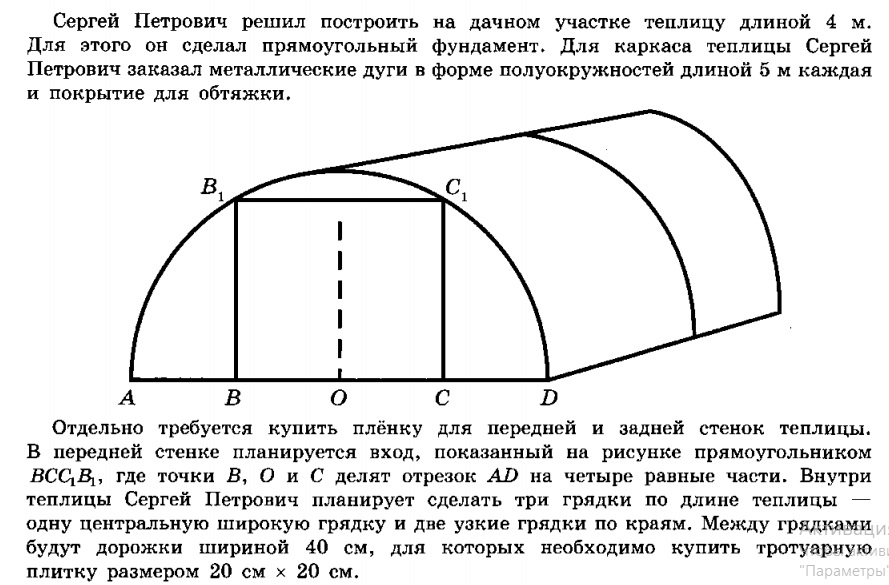
Задание 1 (ОГЭ 2020)
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение: Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).
Ответ: 8.
Задание 2 (ОГЭ 2020)
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продается в упаковках по 6 штук?
Решение: Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки — 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).
Площадь одной плитки: 20 * 20 = 400 (кв. см).
32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.
80 : 6 = 13 (остаток 2).
Понадобится 13 + 1 = 14 упаковок плитки.
Ответ: 14.
Задание 3 (ОГЭ 2020)
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Решение:
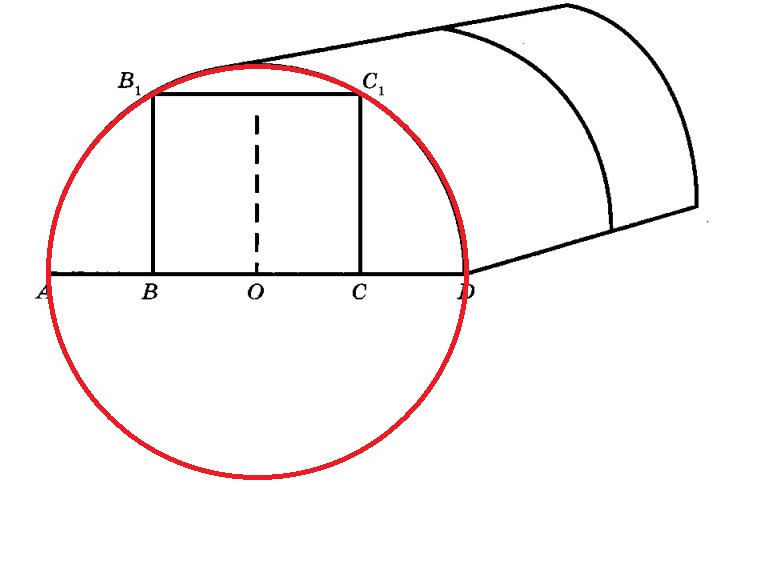
Дуги для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.
Ширина теплицы AD является диаметром окружности. AD = 2 * OD.
Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).
OD = 5 : 3,14 = 1,6 (м).
AD = 2 * OD = 2 * 1,6 = 3,2 (м).
Ответ: 3,2.
Задание 4 (ОГЭ 2020)
Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.
Решение: Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки — 2х см.
Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.
х = 60 (см) — ширина узкой грядки.
Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).
Ответ: 120.
Задание 5 (ОГЭ 2020)
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
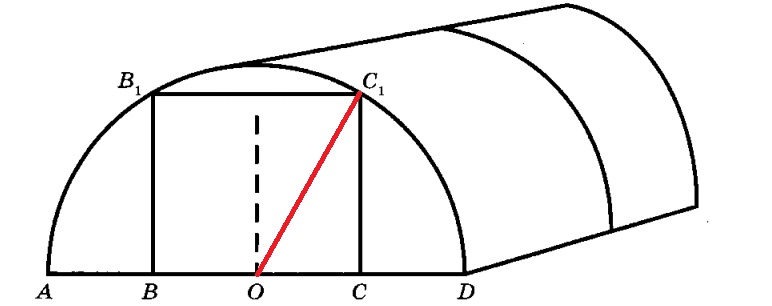
Чтобы найти высоту входа в теплицу,нужно рассмотреть прямоуголный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.
По условию AB = BO = OC = CD = 320 см : 4 = 80 см.
ОС1 = OD = 160 см — радиусы.
По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.
Ответ: 136.
Подробный ОГЭ 2020 — земледелец устраивает на склонах гор терассы — задания 1 — 5.
Источник: mathembox.xyz