Орнаменты, привлекая своей симметрией, довольно часто используются и встречаются в окружающем нас мире. Паркеты же, в свою очередь, играют тоже немаловажную роль. С математической точки зрения орнаменты и паркеты -это покрытия плоскости фигурами, имеющими некоторые общие свойства. Стоит отметить, что не всякий >, даже простой, состоящий из треугольников можно реализовать, как паркет, то есть покрытие плоскости.
В школьных учебниках рассмотрены лишь некоторые элементы, которые используются при построении теории орнаментов и паркетов. В учебниках геометрии 7-9 рассматриваются центральная симметрия, осевая симметрия, поворот и параллельный перенос , правильные многоугольники — понятия, необходимые для конструирования орнаментов и паркетов. Курс алгебры и начал анализа рассматривает периодические функции, их свойства, функцию y=x — первоначальные понятия и объекты, необходимые для построения симметричных и > фигур на плоскости. В работе нам необходимо использовать ещё одну функцию y=x- целая часть числа x, которая помогает упростить уравнения фигур на плоскости, распространяя его на всю плоскость.
Что такое паркет, паркетная и инженерная доска. Виды паркета: плюсы и минусы каждого из них.
Свойства паркетов, а именно возможность построения паркета из простейших фигур — треугольников, представляет собой отдельный интерес, и поэтому, исследование некоторых свойств так же представлено в работе. Основная проблема- подбор и изложение материала, подбор задач, разработка способов их решения, позволили сформулировать тему работы >. И хотя тема предусматривает рассмотрение широкого круга вопросов, большинство из которых уходит вглубь высшей математики, в работе подобран материал, который понятен школьнику и может быть изложен на факультативе.
Работа состоит из введения, четырёх теоретических глав, пятая глава посвящена разбору задач, построению новых упражнений и заданий для самостоятельного решения.
В первой главе рассмотрен способ построения рисунка на плоскости в заданной декартовой прямоугольной системе координат. Здесь на модельном примере рассмотрены типы уравнений, с помощью которых можно задать простейшие фигуры на плоскости.
Во второй главе рассматриваются различные типы орнаментов и способы их построения с помощью уравнений.
Глава третья посвящена классическим покрытиям плоскости правильными многоугольниками, что приводит к понятию правильного паркета.
Четвёртую главу можно считать основной с точки зрения возможности конструирования новых паркетов, потому что она даёт ответ на вопрос существования паркетов из равных треугольников, полученных с помощью разрезаний плоскости.
> множества решений уравнений и неравенств.
Подбирая должным образом уравнения, можно получать самые разнообразные, подчас весьма причудливые картинки3. Например, можно получить > , изображённую на рисунке 1. Как это сделать? Предварительно нам придётся вспомнить, что числовой плоскостью называется множество всех пар действительных чисел. Любое множество точек числовой плоскости условимся называть геометрической функцией, расположенной на числовой плоскости.
Выбор паркета: практические советы от дизайнера
Можно, в частности, рассмотреть множество всех таких пар действительных чисел (x, y), для которых f (x, y) = 0, где f (x, y) — заданное выражение. В этом случае говорят, что получающаяся геометрическая фигура описывается уравнением f (x, y) = 0.
Так уравнение x2-y=0 описывает параболу; уравнение x2 — y2=0 — две прямые (y=x и y= — x), пересекающиеся в точке (0, 0); уравнение x2+y2=2 — окружность с центром в точке (0, 0) и радиусом 2; уравнение x+y = 1 — квадрат с центром в точке (0, 0) и вершинами, лежащих на координатных осях.
Рассмотрим функцию y=cosx. Эта функция чётна (cos-x=cosx) и периодична (cos2PI+x=cosx), поэтому её график обладает зеркальной симметрией относительно оси ординат Oy и состоит из одинаковых периодически повторяющихся кусков.
Мы будем говорить, что график функции y=cosx (его уравнение можно записать так: y-cosx=0) является линейным орнаментом. Таким образом, линейный орнамент получается с помощью переносов некоторой основной фигуры вдоль некоторого направления. Если сам линейный орнамент считать основной фигурой и произвести над ним серию переносов вдоль нового направления, то мы получим двумерный орнамент. Повороты основной фигуры на углы, кратные 3600PI , приводят к круговым орнаментам.
Рассмотрим сначала один простой пример. B качестве основной фигуры F0 взята окружность с центром в начале координат и радиусом r=1, её уравнение в декартовой системе координат: x2+y2=1. Заметим, что все точки окружности (кроме одной) лежат в полосе -1 0, k=0, +-1, +-2. ), описывается уравнением: fx-Tx-aT, y=0. Пусть теперь основная фигура F0 , заданная в полосе b > способом (то есть не таким, когда все точки останутся на своём месте).
Например, повернув всю сетку вершин и сторон, образующих паркет из шестиугольников, квадратов и треугольников, квадратов и треугольников, на 600 вокруг центра одного из шестиугольников, мы получим ту же самую сетку вершин и сторон. Центр каждого шестиугольника этого паркета является >.
Что такое правильный паркет
С точки зрения симметрии наше определение паркета не слишком удачно. Оно допускает паркеты, не обладающие никакой симметрией. Взяв обычный паркет из шестиугольников, можно > его, подразделив некоторые из шестиугольников на шесть треугольников. Легко понять, что получиться вновь > в смысле нашего определения.
Но, подразделив, например, три шестиугольника, оставив все остальные не подразделёнными, мы получим паркет, совсем лишённый симметрии. Чтобы устранить некрасивые, недостаточно симметричные паркеты, мы введём такое определение: Паркет называется правильным, если его можно наложить на самого себя так, что любая заданная его вершина наложиться на любую другую заданную его вершину.
Источник: www.microarticles.ru
Презентация «Паркеты. Правильные, полуправильные» по математике – проект, доклад

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7
Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15
Слайд 16

Слайд 17
Слайд 18

Слайд 19
Презентацию на тему «Паркеты. Правильные, полуправильные» можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на соответствующий текст под плеером.
Презентация содержит 19 слайд(ов).
Слайды презентации

паркеты. правильные, полуправильные.

Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.

Из каких правильных многоугольников можно составить паркет?

попытка №1 ура! получился!

увы. ничего не вышло.


в узле 360 градусов
Необходимое усло-вие для построения паркета.


Возле любого правильного многоугольника можно описать окружность .
В окружность можно вписать правильный многоугольник.
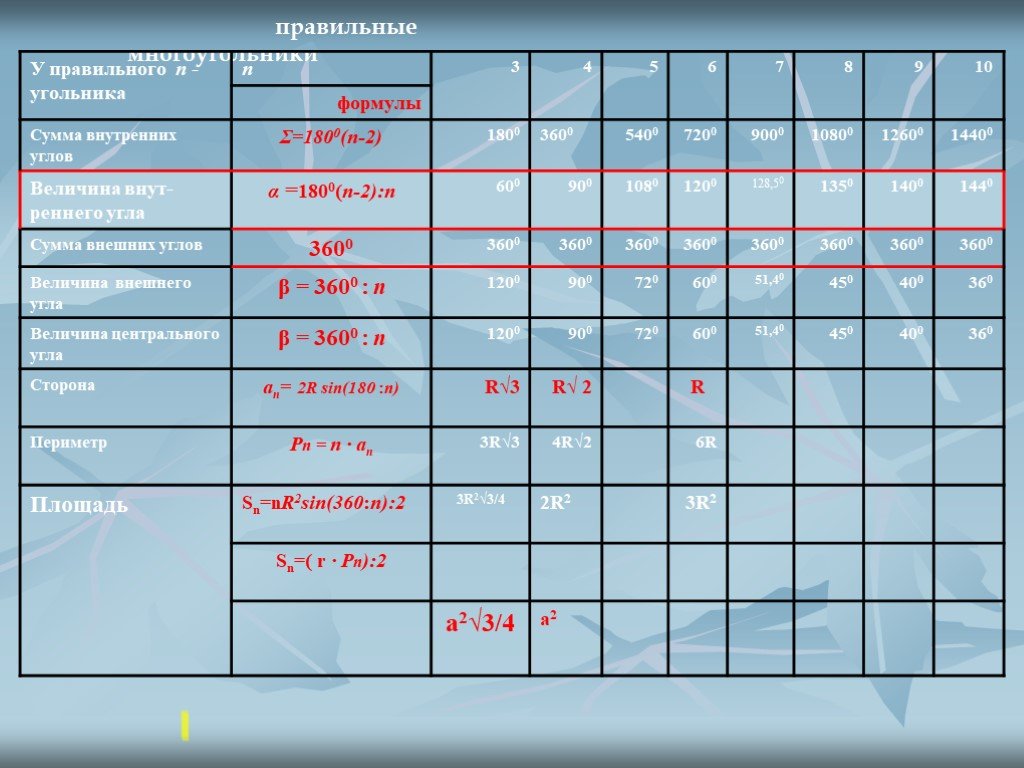
1. при n=3, то m=3600/600=6 треугольников в узле
2.при n=4 ,то m=3600/900=4 четырёхугольника в узле
3.при.n=5, то т=3600:1080=3.333333
При п>7 внутренние углы правильных п-угольников больше 1200. Кроме того внутренние углы правильного многоугольника всегда меньше1800 . 1200 3600/α > 3600/1800 , 2 7 не существует правильных многоугольников для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников построить нельзя!
4 . при n=6 , то m=360:120=3 шестиугольника в узле

Из правильных пятиугольников нельзя сложить паркет.

Только из этих правильных многоугольников можно построить правильный паркет.

из правильных шестиугольников


В УЗЛЕ ГРАДУСОВ
Необходимое условие для построения паркета.

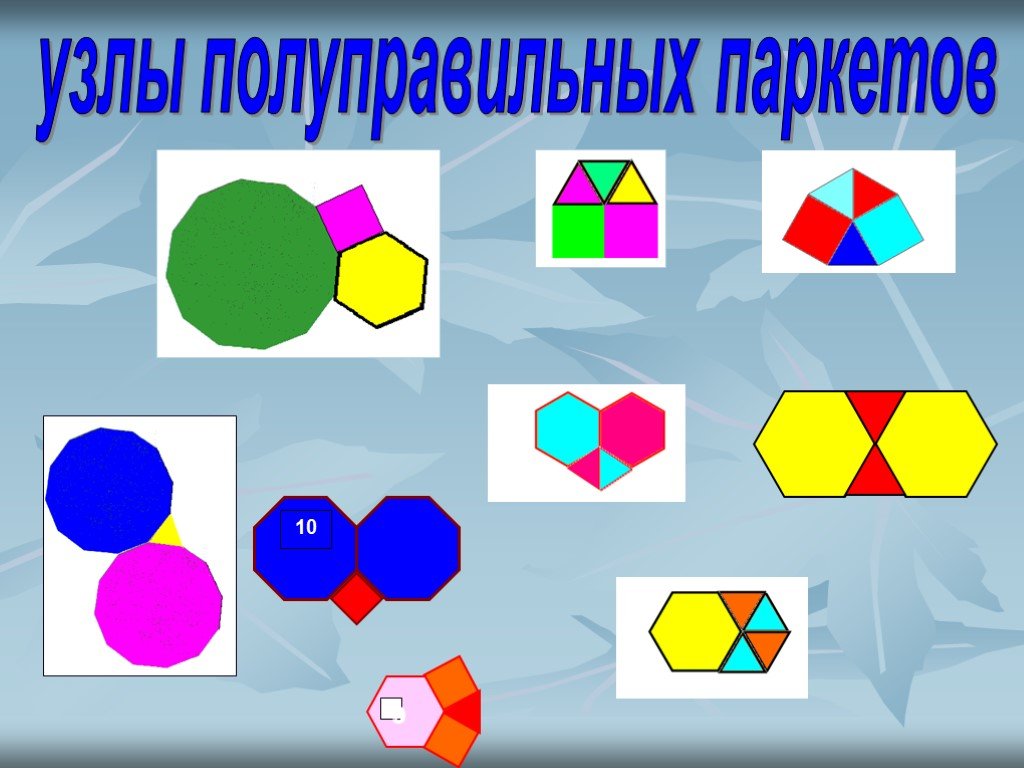
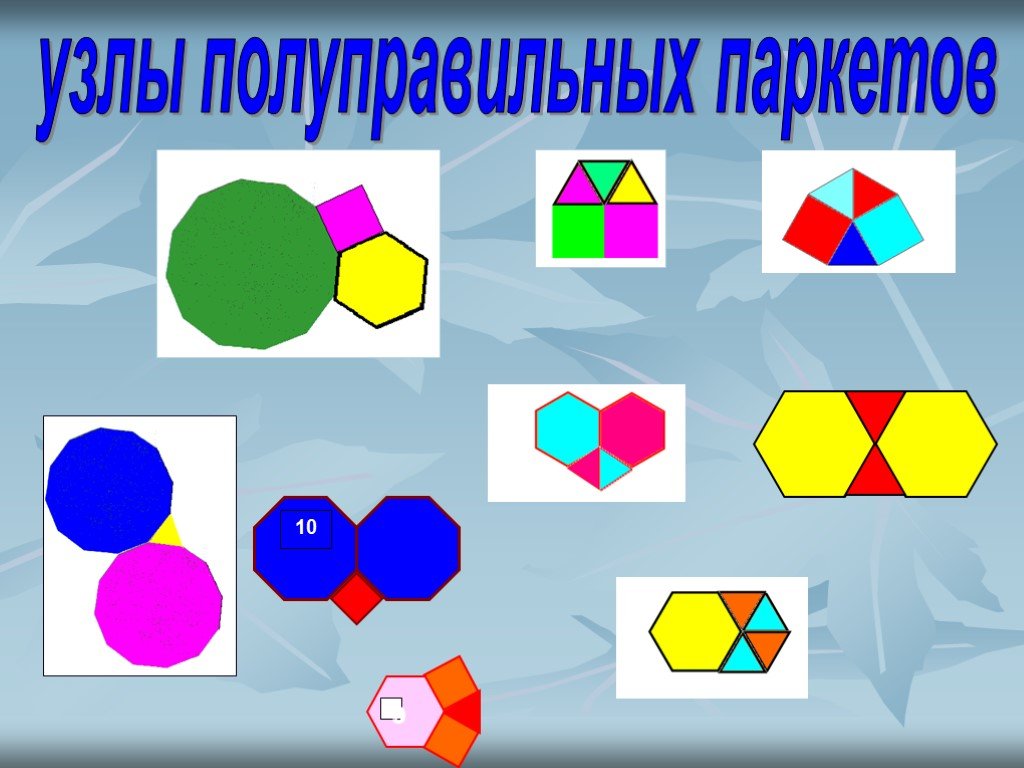
узлы полуправильных паркетов

полуправильный полуправильных паркетов получается 8 видов


Список похожих презентаций

Правильные и полуправильные многогранники
Учение о правильных многогранниках изложил в своих трудах Платон. С тех пор правильные многогранники называют Платоновыми телами. Существует пять .

Правильные многоугольники в природе. Паркеты из правильных многоугольников.
Многоугольники в природе. В природе часто встречаются разнообразные правильные многоугольники. Это могут быть треугольники, четырехугольнике, пятиугольники .

Правильные и полуправильные многогранники
СОДЕРЖАНИЕ. Правильные и полуправильные многогранники Тела Архимеда Леонардо да Винчи. Правильным многогранником называется выпуклый многогранник, .

Правильные многоугольники
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» Я.А.Каменский. Правильным .

Правильные многоугольники
Цель урока:. Закрепить и обобщить полученные знания учащихся при изучении данной темы; 2. Продолжить развитие умения учащихся решать задачи с использованием .

Правильные многоугольники
Разгадав ребус, вы определите тему урока. Правильные многоугольники. «Три качества: обширные знания, привычка мыслить и благородство чувств – необходимы .

Правильные многогранники и их приметы
Многогранник называется правильным если:. 1) ОН ВЫПУКЛЫЙ. (Т.Е. ЛЕЖИТ ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ ГРАНИ). 2) ВСЕ ЕГО ГРАНИ – РАВНЫЕ ПРАВИЛЬНЫЕ .

Правильные многогранники в четырехмерном пространстве
Абстрактный Тороидальный Гексадекаэдр — это комбинаторно-топологический объект — правильная триангуляция тора с 8 вершинами и 16 гранями. С. А. Л., .

Правильные и неправильные дроби
. Какая часть фигуры закрашена? х 1 0. Укажите координаты заданных точек на числовой прямой и на этой числовой прямой отметьте точки А(1/6),В(5/6). .

Симметрия в пространстве. Правильные многогранники
СИММЕТРИЯ В ПРОСТРАНСТВЕ. «Симметрия … есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман .

Правильные и неправильные дроби 5 кл
Цели урока:. Сегодня на уроке я хочу: Узнать…. Научиться….. Составлять…. Понять…….
Сравнение дробей. С одинаковыми знаменателями С одинаковыми числителями .

Правильные и неправильные дроби
В этом заборе 4 доски закреплены ненадежно. На них написаны неправильные дроби. Найди их. Не ошибайся. Твои ошибки увидят все. Выбери справа доски .

Правильные и неправильные дроби

Правильные и неправильные дроби
Задачи урока:. Познакомиться с понятиями «правильная» и «неправильная» дробь; упражняться в составлении и записи правильных и неправильных дробей, .

Правильные и неправильные дроби
Запиши с помощью дроби:. Какую часть метра составляют: 1 дм, 9 дм, 1 см, 27 см? Какую часть тонны составляют: 1 кг, 16 кг, 1 ц, 85 ц? Какую часть .

Правильные и неправильные дроби
Решите ребус и расшифруйте анаграммы. Ребус 2,, ,, ь 2. ИТЛИЬЛЕСЧ 3.АМЗТЕЛЬНАЕН. ТЕМА УРОКА. Правильные и неправильные дроби. Знания Применение. Уметь .

Правильные многоугольники в нашей жизни
Правильный треугольник. Правильный четырёхугольник. Правильный шестиугольник. Правильный пятиугольник. Правильный восьмиугольник. .

Правильные многогранники
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. .

Правильные многоугольники задачи
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. Определение правильного многоугольника Описанная и вписанная окружность Формулы для вычисления площади Упражнения и задачи .

Правильные многогранники в геометрии
Цели: Знакомить учащихся с новым типом многогранников — правильными многогранниками. Показать влияние правильных многогранников на возникновение филосовских .
Конспекты
Правильные многогранники
2. . . Конспект урока геометрии с применением ИКТ в 10 классе. Тема:. Правильные многогран. ники. Цели урока:. Предметный компонент:. Изучение .
Правильные многогранники
Урок геометрии в 11 классе. «Правильные многогранники». Учитель математики КГУ «Гимназия №6 г. Семей» Бочарова Галина Борисовна. Цель: Знакомство .
Правильные многогранники
Тема урока: «Правильные многогранники». (10 класс). Учитель математики Иманова Алена Викторовна. МБОУ «Средняя общеобразовательная школа №21». .
Правильные многогранники
Урок по теме: «Правильные многогранники». Тип урока:. изучение нового материала. Продолжительность урока. : 2 урока по 45 минут. Цель урока:. .
Правильные и неправильные дроби
Правильные многогранники
Муниципальное общеобразовательное учреждение. . средняя общеобразовательная школа №5. Урок геометрии в 11 классе. «Правильные многогранники». .
Правильные и неправильные дроби
План-конспект урока. . Учителя. математики и информатики. . МБОУ СОШ. №20. ФИО. Лютова Ирины Сергеевны. . Класс: 5. Предмет: математика. .
Правильные многоугольники
ФИО автора материала: Мосолкова Людмила Васильевна. . Место работы (название образовательного учреждения: МБОУ г. Магадана «СОШ с УИМ № 15». . .
Правильные и неправильные дроби
Государственное специальное (коррекционное) образовательное учреждение для обучающихся (воспитанников) с отклонениями в развитии, школа-интернат I .
Правильные и неправильные дроби
Солдатова. . Ирина Валерьевна. I. квалификационная категория. Самарская область Исаклинский район с. Исаклы. ГБОУ СОШ с. Исаклы. Математика. .
Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Источник: prezentacii.org
Исследовательская работа учащегося «Паркет: геометрия и искусство»
В основе любого паркета лежит математическая строгость организации
формы, простая или усложненная система поворотов, узор, который строится на симметрии. Для того чтобы создать собственный вид паркета, необходимо изучить уже существующие виды паркетов и то, как они создаются.

Оценить 1748 0
Содержимое разработки
Муниципальное автономное образовательное учреждение
«Средняя общеобразовательная школа №6 имени Героя России
С.Л. Яшкина» г. Перми
Паркет: геометрия и искусство
Выполнила
Туманова Анна,
ученица 8 «В» класса
Руководитель
Орлова Елена Валентиновна,
2. Геометрические паркеты5
2.1 Правильные паркеты6
2.2 Полуправильные паркеты7
2.3 Паркеты из неправильных многоугольников8
3. Паркеты из произвольных фигур 8
4. Паркет для комнаты9
Введение
Математика несет красоту в любую науку
Математика является необходимой частью жизни человека, ведь математические знания применяются во всех сферах жизни. Так знания геометрии широко используются в создании новых зданий, дорог, мостов и многого другого. Безусловно, математика даёт нам возможность применить знания и в украшении окружающего мира. Мы повсюду видим красивые дорожки парков, площадей, улиц, а также тротуары, которые украшает интересная плитка. Наш взгляд привлекают оригинальные паркеты в интерьерах.
В основе любого паркета лежит математическая строгость организации
формы, простая или усложненная система поворотов, узор, который строится на симметрии. Для того чтобы создать собственный вид паркета, необходимо изучить уже существующие виды паркетов и то, как онисоздаются.
Целью данной работы является изучение геометрических приемов составления паркетов.
Для достижения данной цели необходимо решить следующие задачи:
изучить литературу по данной теме;
ознакомиться с геометрическими приёмами составления паркетов;
разработать собственный паркетный узор
рассчитать количество и стоимость материалов, необходимых для укладки паркета в комнате.
1. Сквозь века
Паркет (наборный деревянный пол) относится к наиболее древним видам напольных покрытий: согласно историческим свидетельствам, наборные деревянные полы использовались еще в Древнем Египте, то есть около 5 тысяч лет тому назад [3]. Высоко ценили паркетные полы императоры китайских династий, высшая персидская знать и представители многих других цивилизаций.
Само слово «паркет» пришло в русский язык из французского языка. Однако в средние века во Франции им обозначали небольшой парк, немного спустя — предназначенную для аудиенций часть зала, покрытую ковром. Ковры постепенно исчезли, паркетные полы стали частью интерьера, так же искусно выполненной, как настенные гобелены.[7]
История паркета в России начинается приблизительно с XVI столетия — когда помимо настилаемых дощатых полов, состоящих из больших массивных досок во всю длину помещения, начали изготавливаться напольные покрытия из так называемых «дубовых кирпичей», вырезаемых из досок дуба. Подобные полы получили название «косящатых», поскольку укладывались именно знаменитым рисунком «елочкой». Их выкладывали на грубо сработанное основание из мягких пород древесины — преимущественно сосны. Дальнейшее развитие художественного паркета в России привело к использованию щитового паркета, когда узоры попусту набирались в щиты размером 1,5х1,5 метра и выкладывались на основу. Для изготовления паркета и наряду с местными отечественными породами: березой, орехом, сосной, лиственницей, кленом, дубом, буком, грабом, ясенем, вязом, грушей, яблоней, ольхой, можжевельником, карагачем и кизилем — стали все более и более применять редкие и дорогостоящие сорта привозных «заморских» деревьев: фиолетовый палисандр, розовый амарант, желтое и красное сандаловое дерево, шелковицу, черное эбеновое, оливковое дерево и др.[12]
Художественный паркет выполняли обычно 2 способами — интарсией, которая предполагала инкрустацию, и маркетри, которая состояла в наборных работах. [11]
В начале 18 века в России доминировал стиль раннего барокко и мода на геометрические рисунки паркета — кубы, ромбы, квадраты, кресты, многолучевые звезды, составляющие основное поле пространства пола, что определялось помимо художественных предпочтений простотой способ изготовления — требовались только прямые резы планок. Все производство паркета вплоть до конца 19 века выполнялось ручным способом. Лишь к началу 20 века ряд фабрик приступили к массовому промышленному производству простых паркетных планок из различных пород древесины. Сегодня детали паркета вырезаются на станках и с применением лазера и компьютера.[12]
В настоящее время выделяют следующие разновидности паркета: штучный, наборный (мозаичный), щитовой, дворцовый (художественный), массивный [10] (Приложение 1).
Геометрические паркеты
В геометрии паркетом называют замощение плоскости многоугольниками, при котором вся плоскость оказывается покрытой ими без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек.[9] С паркетами мы встречаемся в повседневной жизни.
Паркетами покрывают не только полы в домах, но и украшают ими стены комнат и зданий. Для создания интерьеров используются изделия выполненные из лоскутов материи, Издавна на Руси вяжут пуховые платки напоминающие паркеты (Приложение 2). Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Можно придумать сотни, тысячи разных элементов паркета.
2.1 Правильные паркеты
Правильным (Платоновыми) паркетом называется паркет, составленный из равных правильных многоугольников, и вокруг каждой вершины правильного многоугольника многоугольники расположены одним и тем же способом.[2] (Приложение 2)
В природе и в жизни мы часто имеем дело с правильными паркетами. Например: шахматная доска и пчелиные соты (Приложение 2). Эти предметы состоят из многоугольников с равными углами и равными сторонами. Шахматная доска – паркет из правильных четырехугольников. Пчелиные соты – паркет из правильных шестиугольников.
Пчелы бессознательно решают математическую задачу – они стараются придать сотам такую форму, чтобы при заданном объёме на них шло как можно меньше воска. И хотя они не знают математики, но точно решают эту задачу. Пчелам помогает решать эту задачу инстинкт. В свою очередь, правильные шестиугольники состоят из правильных треугольников, поэтому паркеты из правильных треугольников тоже существуют. Задача о замощении плоскости правильными треугольниками, квадратами и шестиугольниками была известна еще древним грекам. Позже было доказано, что выложить паркет из других видов правильных многоугольников нельзя, так как геометрические фигуры могут «встретиться» в вершине паркета только тогда, когда сумма их углов составляет 360 градусов, иначе они не сомкнуться вокруг вершины или «налезут» друг надруга.[1]
Пусть в каждой точке плоскости сходятся m одинаковых правильных n-угольников, то должно выполняться равенство:
m*180º*(n-2)/n=360º (величина угла правильного n-угольника равна 180º*(n-2)/ n)
После преобразований получим: m=2*n/(n-2).
Если n=3, m=6 (6 треугольников в узле).
Если n=4, m=4 (4 четырёхугольника в узле).
Если n=5, m=3,333333… Но m не может быть дробным числом, число многоугольников должно быть натуральное.
Значит, пятиугольниками заполнить плоскость нельзя.
Если n=6, m=3 (3 шестиугольника)
Для п ≥ 7 не существует правильных многоугольников, для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников (п > 7; 8; 9… ) построить нельзя! [2]
Полуправильные паркеты.
Самые простые паркеты складываются из одинаковых правильных многоугольников, имеющих одинаковые же стороны и углы. Используя две или больше фигур, можно замостить полуправильный паркет.
Полуправильными (архимедовыми) паркетами называются паркеты, состоящие из правильных многоугольников двух или более типов, такие, что для любых двух вершин паркета существует преобразование симметрии (самосовмещение), переводящее одну из них в другую. (Приложение 2)
Сумма углов правильных многоугольников, сходящихся в одной вершине, равна 360 0 . Поэтому в вершине паркета может сходиться не мене 3 и не более 6 многоугольников. Это объясняется тем, что если в одной вершине сходятся два многоугольника, то внутренний угол одного из них должен быть более 180 0 , но это невозможно. Аналогично, если предположить, что в одной вершине сходятся семь многоугольников, то у одного из них внутренний угол должен быть менее 60 0 . А это также невозможно, так как 60 0 -минимальный угол правильного многоугольника (треугольника).[2]
Существует всего 8 видов паркетов, составленных из нескольких правильных многоугольников разной формы [8]:
1) с 3-мя многоугольниками в вершине (Приложение 2 рис.9-11);
2) с 4-мя многоугольниками в вершине (Приложение 2 рис.12-13);
3)с 5-ью многоугольниками в вершине (Приложение 2 рис.14-16).
2.3 Паркеты из неправильных многоугольников
Впрочем, правильными многогранниками геометрия не ограничивается. Если мы не станем упираться в такие фигуры, а сможем использовать любые, возможных паркетов станет бесконечное множество.
Легко покрыть плоскость параллелограммами. (Приложение 3. Рис.9)
Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого (Приложение 3. Рис. 10).
Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника». В то же время существуют паркеты из невыпуклых семиугольников (Приложение 3. Рис.10)[5]
Мы можем отказаться даже от симметрии переноса, выкладывая плитку сложным узором: если такую картинку куда-нибудь сдвинуть, она никогда не совпадет с исходной. Такие непериодические паркеты можно выкладывать с помощью самых разных фигур. Классические исследования на эту тему во второй половине ХХ века провел знаменитый английский математик Роджер Пенроуз, описавший три типа мозаик, в которых используется от двух до шести разных фигур, замощающих плоскость без промежутков, при этом рисунок не повторяется никогда. В мозаике Пенроуза (Приложение 3. Рис.12) невозможно найти «минимальный» рисунок, который, будучи скопированым, замостил бы плоскость без промежутков. Тем удивительнее, что сама мозаика, не повторяясь, замощает ее целиком [12].
Паркеты из произвольных фигур
Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае — многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми). В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур.[6]
Наиболее яркими примерами таких паркетов являются работы голландского художника Мориса Эшера, который говорил «Хотя я абсолютно несведущ в точных науках, мне иногда кажется, что я ближе к математикам, чем к моим коллегам-художникам». Элементами паркета у него служили фигуры животных, птиц,рептилий.(Приложение 4)
Исходя из «расширенного» определения рассмотрим способы построения нового паркета.[6]
1) Необходимо взять уже известный паркет (удобнее всего паркет, состоящий из прямоугольных четырехугольников, так называемой «сетки»). Сжимая или растягивая отрезки «сетки», заменяем прямолинейные отрезки кривыми с началом и концом в тех же точках, что и уотрезков;
2) Объединить отдельные элементы уже существующих паркетов;
3) Существующую «сетку» дополнить новыми линиями;
4) Наложить друг на друга несколько «сеток», сместив и/или повернув их, чтобы получился необычный замкнутый контур.
Изучив виды паркетов и способы их построения я создала свои паркеты (Приложение 5).
Паркет для комнаты
Знания геометрии помогают при проведении отделочных работ, в частности, при укладке пола паркетом.
Сначала замеряется площадь пола помещения, в котором будет происходить монтаж напольного покрытия, а затем рассчитывается необходимое количество доски. Это число зависит от направления укладки. При монтаже паркета по прямой к стене, необходимо купить материала примерно на 7% больше площади помещения, при диагональной укладке, увеличение от площади пола составит около 15%. Варианты раскладки паркета в Приложении 6.
Ниже приведен сравнительный анализ стоимости паркета в магазинах г.Перми
Источник: www.prodlenka.org