Пол комнаты ,имеющий форму квадрата со стороной 4 м,нужно покрыть паркетом прямоугольной формы.Длина каждой дощечки паркета равна 20 см,а ширина -10 см.Сколько дощечек потребуется?
![]() 42
42 ![]() 0
0
Комментарии (0)
По дате По дате Популярные
Нет комментарий
Войдите, чтобы комментировать
Ответов нет
![]()
Знаешь ответ? Добавь его сюда и заработай денег! Ответы проходят модерацию. Минимум 100 символов.
Чтобы добавить ответ — нужно войти или зарегистрироваться
Похожие вопросы
(Онуфрий Васильев ученик ) (Геометрия)
![]()
1
(Марианна Краснова ученик ) (Геометрия)
![]()
1
(Егор Морозов ученик ) (Геометрия)
![]()
Дачный участок имеет форму квадрата … | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРА
1
(Созон Титов ученик ) (Геометрия)
![]()
1
(Лукьян Галкин ученик ) (Геометрия)
![]()
1
Источник: teachs.ru
Алекс Ларин 165 вариант решение 1 части геометрия
Разбираем с сайта Алекс Ларин 165 вариант решение 1 части блока геометрия, задания 15 -20. Каждое задание этого блока оценивается в 1 балл.
Алекс Ларин 165 вариант решение 1 части геометрия
Задание 15
Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см.
Сколько потребуется таких дощечек?
Переведем измерения дощечек паркета из см в м.
5 см = 0,05м, 20 см = 0,2 м.
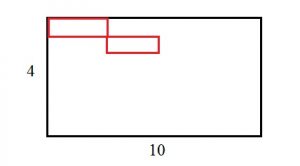
У прямоугольника противоположные стороны равны.
Найдем сколько дощечек умещается в длину 10 : 0,2 = 50 (штук).
Найдем сколько дощечек умещается в ширину пола комнаты 4 : 0,05 = 80 (штук).
Всего дощечек 50 · 80 = 4000.
Задание 16
На прямой АВ взята точка М. Луч MD — биссектриса угла CMВ. Известно, что
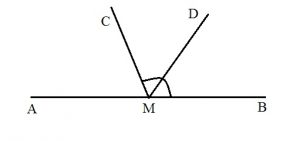
Так как MD — биссектриса угла CMB, то
Сумма смежных углов составляет 180 градусов. Следовательно,
Задание 17
Катеты прямоугольного треугольника равны 7 и 24. Найдите гипотенузу этого треугольника.
Используя формулы прямоугольного треугольника — Теорему Пифагора, находим гипотенузу этого треугольника: 25.
Задание 18
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 12. Найдите площадь треугольника ABC.
Дачный участок имеет форму прямоугольника … | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 8 | ШКОЛА ПИФАГОРА
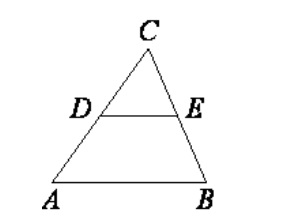
Так как DE — средняя линия, то она параллельна основанию треугольника AB и равна половине основания. DE = AB:2.
Треугольники DCE и ACB подобны по двум углам( угол А общий и углы CDE и CAB равны как соответственные при параллельных прямых AB и CB и секущей AC) с коэффициентом подобия 1/2.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Здесь подробно рассмотрено решение 19 задания и 24 задания 165 варианта Алекс Ларин.
Задание 20
Какие из следующих утверждений верны?
1. Площадь квадрата равна произведению двух его смежных сторон.
2. Диагональ трапеции делит её на два равных треугольника.
3. Если две стороны одного треугольника соответственно равны двум сторонам
другого треугольника, то такие треугольники равны.
Правильный ответ под номером 1.
Источник: mathembox.xyz
Пол комнаты ,имеющий форму квадрата со стороной 4 м, нужно покрыть паркетом прямоугольной формы. длина каждой дощечки паркета равна 20 см, а ширина -10 см. сколько дощечек потребуется?

1. проведем ао1 — искомое расстояние. проведем оо1 — высоту призмы.
оо1 = 1, стороны оснований призмы равны : а = 4.
ао — половина диагонали основания и равна (акор2)/2 = 2кор2.
из пр. тр-ка ао1о найдем ао1 по теореме пифагора:
2. построим тр-ик ас1в. он равнобедренный ас1 = вс1 = кор(1+1) = кор2
ав = 1. проведем высоты с1к на основание ав и искомую высоту ам на боковую сторону вс1. пусть с1к = h, am = h = ?
найдем сначала h:
из пр.тр. ас1к: h = кор(2-(1/4)) = (кор7)/2
тогда площадь авс1: s = (1/2)*1*(кор7)/2 = (кор7)/4
с другой стороны: s= (1/2)*(кор2)*h
приравняв, получим: h= (кор7)/(2кор2) = (кор14)/4
а) строим тр-ик ав1д1. он равносторонний, его стороны — диагонали граней куба и они равны кор2.
искомое расстояние — высота этого равностороннего тр-ка.
h = (кор2)*(кор3)/2 = (кор6)/2.
б) строим тр-ик аа1с. он прямоугольный. катеты аа1 = 1 и ас = кор2.
гипотенуза — диагональ куба а1с = кор(1+1+1) = кор3
в надо найти высоту, опущенную на гипотенузу:
h = ab/c = (кор2)/(кор3) = (кор6)/3.
в) это расстояние до другой диагонали куба. оно точно такое же, как в п.б)
Источник: reshebnik-gdz.com