Исполнитель Черепаха умеет делать рисунки и чертить на плоскости. Поскольку ей нужны все ее лапы, чтобы ходить, она держит перо в зубах.
Среда Черепахи – плоскость с системой координат. Система координат необходима для того, чтобы однозначно определять место Черепахи на плоскости. Черепаха редко использует прямоугольную систему координат, она поступает так же, как и человек – может развернуться в любую сторону и идти вперед или назад. Такая система координат (“вправо-влево-вперед-назад”) называется естественной системой координат.
Какие команды понимает Черепаха?
СКИ Черепахи:
покажись; Черепаха появляется на экране
скройся; Черепаха исчезает
опусти_перо; Черепаха оставляет за собой след
подними_перо; Черепаха перемещается без следа
в_точку ( x, y ); переместиться в точку с координатами (x,y)
вперед ( n ); переместиться вперед на n шагов
назад ( n ); переместиться вперед на n шагов
влево ( a ); развернуться влево на угол a градусов
Уроки на языке Pascal. Урок 18. Динамические переменные и указатели.
вправо ( a ); развернуться вправо на угол a градусов
Как видно из этого списка команд, для Черепахи важно не только ее начальное положение на плоскости, но и ее направление. Мы будем считать, что в исходном положении Черепаха смотрит вверх (“на север”).
Как управлять Черепахой?
Сначала выполним простейшую задачу для Черепахи — нарисуем квадрат со стороной 40 шагов. Черепаху будем обозначать черным треугольником. Как вы знаете, все углы квадрата равны 90 градусов, поэтому программа выглядит так:
вперед ( 40 ); вправо ( 90 );
вперед ( 40 ); вправо ( 90 );
вперед ( 40 ); вправо ( 90 );
Как раскрасить рисунок?
Вы заметили, что Черепаха рисует все время черной линией. Используя специальные команды, рисунок можно раскрасить.
- Для изменения цвета линии используется команда
цвет ( n ); /* установить цвет линии n */
Цвет линии может иметь значения от 0 до 15, таким образом можно использовать всего 16 цветов:
Источник: studfile.net
Исполнитель Черепаха рисует геометрические фигуры в Кумире с использованием циклического алгоритма


Исполнитель Черепаха рисует геометрические фигуры в

Исполнитель Черепаха рисует геометрические фигуры в Кумире с использованием циклического алгоритма
Циклический алгоритм Циклический алгоритм — это описание повторяющихся действий

Подпрограммы в Pascal
Циклический алгоритм — это описание повторяющихся действий.
Список повторяющихся действий называется телом цикла.
В общем виде конструкция повторения записывается
нц раз
кц
Черепаха алг Квадрат нач вперед(100) вправо(90) вперед(100) вправо(90) вперед(100) вправо(90) вперед(100) вправо(90) кон

использовать Черепаха
алг Квадрат
нач
вперед(100)
вправо(90)
вперед(100)
вправо(90)
вперед(100)
вправо(90)
вперед(100)
вправо(90)
кон
Черепаха рисует квадрат. Второй способ (вспомогательный алгоритм)
использовать Черепаха
алг Квадрат
нач
Сторона и угол
Сторона и угол
Сторона и угол
Сторона и угол
кон
алг Сторона и угол
нач
вперед(100)
вправо(90)
вперед(100)
вправо(90)
вперед(100)
вправо(90)
вперед(100)
вправо(90)
кон
Черепаха рисует квадрат. Первый способ (линейный алгоритм)
Блок-схема циклического алгоритма
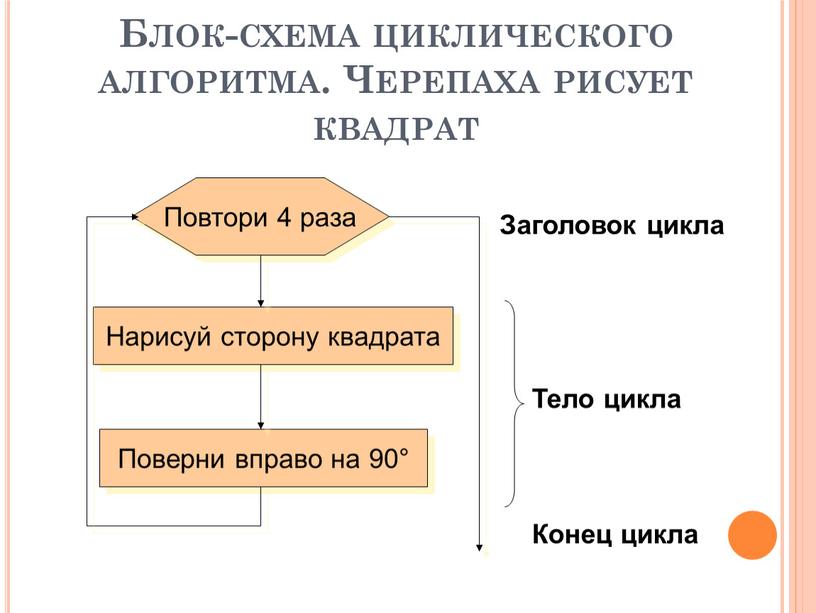
Блок-схема циклического алгоритма. Черепаха рисует квадрат
Черепаха алг Квадрат нач нц 4 раз вперед(100) вправо(90) кц кон

использовать Черепаха
алг Квадрат
нач
нц 4 раз
вперед(100)
вправо(90)
кц
кон
Черепаха рисует квадрат. Четвертый способ (циклический+вспомогательный алгоритмы)
использовать Черепаха
алг Квадрат
нач
нц 4 раз
Сторона и угол
кц
кон
алг Сторона и угол
нач
вперед(100)
вправо(90)
кон
Черепаха рисует квадрат. Третий способ (циклический алгоритм)
Правильный многоугольник Правильный многоугольник — это многоугольник, у которого все стороны и углы равны
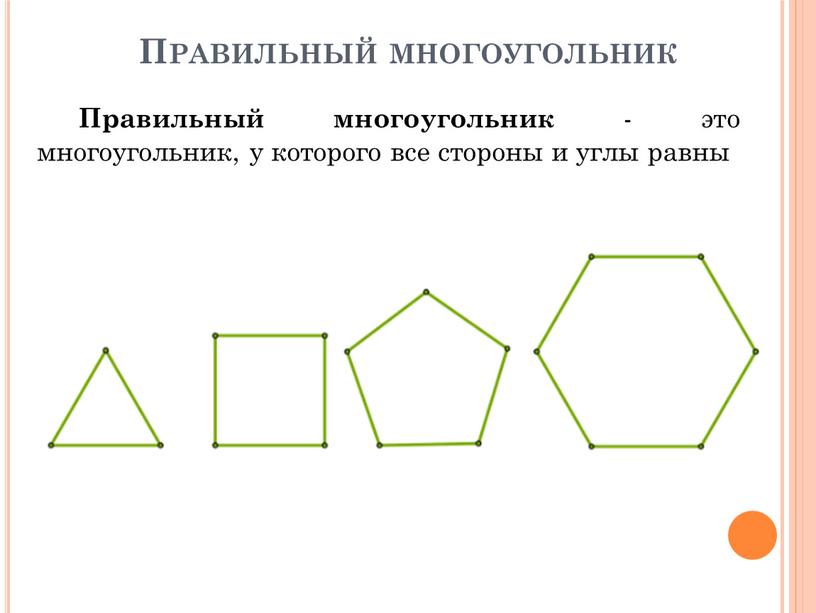
Правильный многоугольник — это многоугольник, у которого все стороны и углы равны
Треугольник Сумма углов треугольника равна 180°
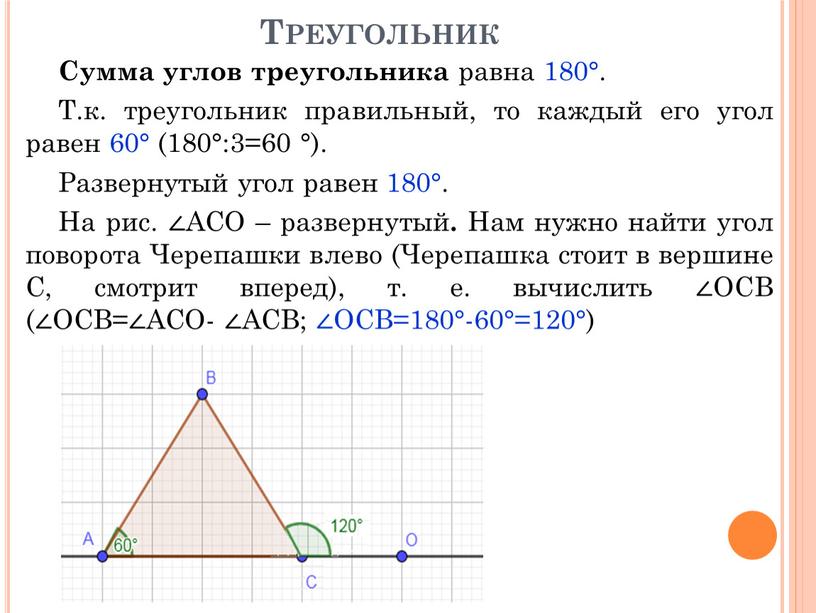
Сумма углов треугольника равна 180°.
Т.к. треугольник правильный, то каждый его угол равен 60° (180°:3=60 °).
Развернутый угол равен 180°.
На рис. ∠АСО – развернутый. Нам нужно найти угол поворота Черепашки влево (Черепашка стоит в вершине С, смотрит вперед), т. е. вычислить ∠ОСВ (∠ОСВ=∠АСО- ∠АСВ; ∠ОСВ=180°-60°=120°)
Найдем закономерность Многоугольник
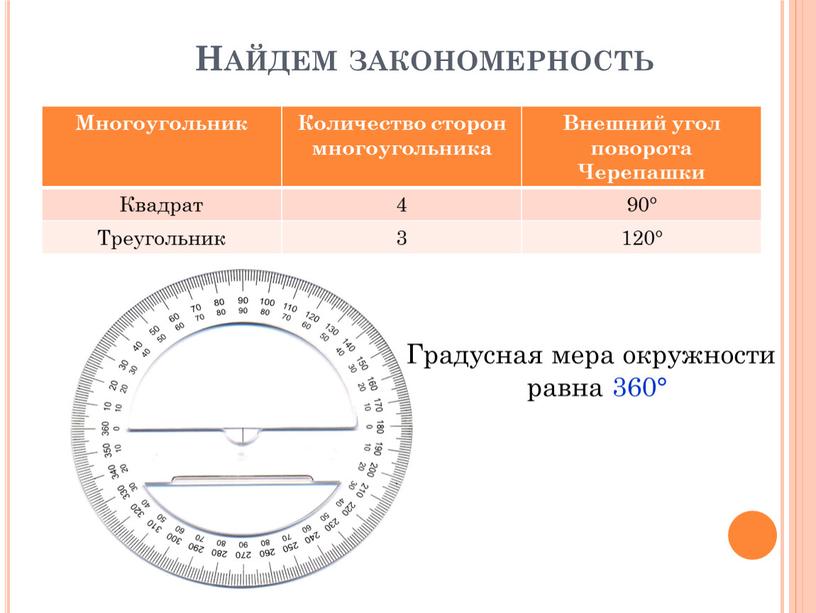
Количество сторон многоугольника
Внешний угол поворота Черепашки
Градусная мера окружности
равна 360°
Формула вычисления внешнего угла правильного многоугольника

Формула вычисления внешнего угла правильного многоугольника
При рисовании правильного многоугольника необходимо поворачивать Черепашку на угол, который можно вычислить по формуле
Угол = 360°:К,
где К – количество углов многоугольника.
Таким образом, для построения пятиугольника угол, на который нужно повернуться Черепашке, равен 360°:5=72°.
Черепаха алг Окружность нач нц 360 раз вперед(1) вправо(1) кц кон

использовать Черепаха
алг Окружность
нач
нц 360 раз
вперед(1)
вправо(1)
кц
кон
Если менять количество повторений и градус поворота, то можно получить разные узоры
использовать Черепаха
алг Полуокружность
нач
нц 180 раз
вперед(1)
вправо(1)
кц
кон
использовать Черепаха
алг Петля
нач
нц 180 раз
вперед(1)
вправо(1)
кц
вправо(90)
нц 180 раз
вперед(1)
вправо(1)
кц
кон
Задания для самостоятельного выполнения
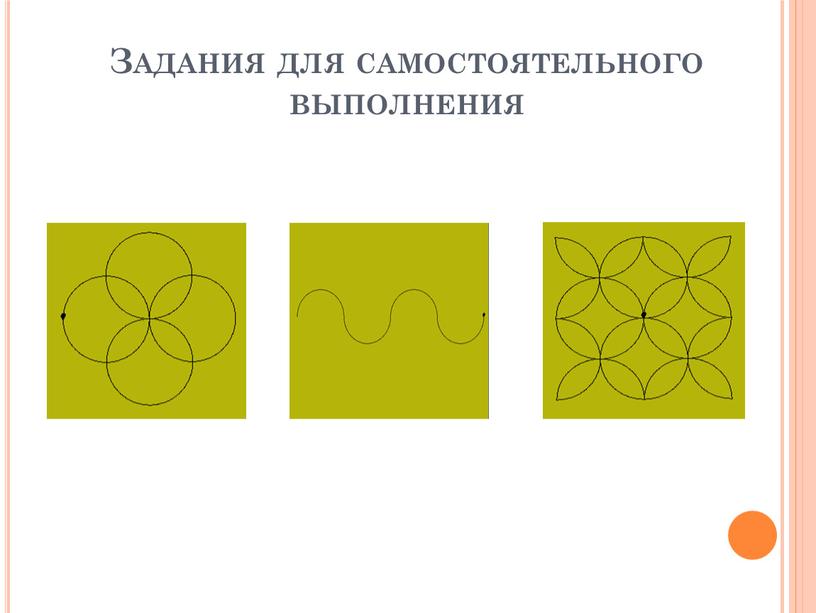
Задания для самостоятельного выполнения
Решение для задач самостоятельного выполнения

Решение для задач самостоятельного выполнения
Источники информации: Информатика: учебник для 6 класса/

Информатика: учебник для 6 класса/ Л.Л. Босова, А.Ю. Босова.- М.: БИНОМ. Лаборатория знаний, 2014.
Информатика. Изучаем алгоритмику. МойКуМир.5-6 классы/Е.А. Мирончик, И.Д. Куклина, Л.Л. Босова. – М.: БИНОМ.
Лаборатория знаний, 2018.
https://uventa-shop.ru/543-thickbox_default/0336410360.jpg — изображение транспортира.
https://www.math10.com/ru/geometria/geogebra/fullscreen.html — бесплатное он-лайн геометрическое приложение для рисования геометрических фигур.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Источник: znanio.ru
Паркеты использование переменных параметры подпрограмм команды повтори вперед вправо
Иногда в задании явно есть одинаковые операции, но применить цикл не удается. Рассмотрим такой рисунок из равносторонних треугольников:

С одной стороны, все треугольники одинаковые, с другой — они расположены так, что нельзя использовать один цикл для всех трех фигур.
Теперь представим себе, что у Черепахи уже есть команда треугольник, которая рисует треугольник и возвращает исполнителя в исходное положение, причем Черепаха должна стоять в углу треугольника и смотреть в ту сторону, в которую она пойдет.
Учтем, что в равносторонних треугольниках все внутренние углы по 60 градусов. Тогда решение может быть записано так:
ТриТреугольника
вправо ( 30 );
треугольник ;
вправо ( 120 ); назад ( 20 ); /* идем ко второму */
треугольник ;
вперед ( 20 ); влево ( 60 ); /* идем к третьему */
вперед ( 40 ); влево ( 60 );
назад ( 20 );
треугольник ;
Если ввести такую программу, то мы получим ошибку «Не понимаю, что такое треугольник». Это и понятно, поскольку такой встроенной команду у Черепахи нет и она не знает, что делать. Поэтому ей надо объяснить, что такое треугольник, написав расшифровку этой команды. Так как внутренние углы равностороннего треугольника равны 60 градусов, Черепаха должна поворачиваться на 180-60=120 градусов.
Треугольник
опусти_перо;
повтори ( 3 )
вперед ( 40 );
вправо ( 120 );
>
подними_перо;
Отдельно взятая программа ТриТреугольника работать не будет, однако если к ней добавить текст вспомогательного алгоритма треугольник, то исполнитель сможет ее выполнить.
Процедуры (вспомогательные алгоритмы, подпрограммы) – это новые команды, которые мы добавляем к СКИ исполнителя. Чтобы исполнитель знал, что делать по этой команде, после основной программы надо дать расшифровку процедуры через уже известные исполнителю команды.
Как правильно применять процедуры?
Процедуры используются в том случае, если исполнителю приходится несколько раз выполнять одни и те же действия. При этом удобно просто ввести новую команду и расшифровать ее один раз — это может значительно сократить текст программы.
Основная программа всегда записывается первой. Она использует новые команды, расшифрованные после нее, при этом говорят, что процедура вызывается. Одна процедура может вызывать другую процедуру.
Если исполнитель встретил новую команду, которой нет в СКИ, он ищет ее расшифровку, выполняет все действия, которые там указаны, и затем продолжает выполнять основную программу со следующей строчки. При этом говорят, что исполнитель возвращается в основную программу после выполнения процедуры.
Практические задания
Составить программу с использованием процедуры для рисования:
 |
 |
Использован материал из книги «Алгоритмы и исполнители», автор Поляков К.
Источник: www.turbopro.ru