Среди огромного разнообразия орнаментов выделяются «паркеты» (мозаики). Паркетом называют заполнение плоскости одинаковыми фигурами (элементами паркета), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда паркетом называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками).
Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Элементом паркета является также равносторонний треугольник, правильный шестиугольник, произвольный параллелограмм, даже произвольный четырехугольник. Можно придумать сотни, тысячи разных элементов паркетов.
Придуманы паркеты, у которых несколько элементов образуют фигуру, подобную элементу паркета.
Замечательные паркеты придумывал знаменитый голландский художник Морис Эшер. Элементами паркета у него служили фигуры животных, птиц, рептилий.
Из всех работ Эшера лучше всего известные его орнаменты (или мозаика), то есть периодическое заполнение плоскости одинаковыми фигурами.
✓ Лайфхак: задачи на растворы/сплавы за 5-10 секунд | ЕГЭ. Задание 9. Математика | Борис Трушин
Морис Эшер интересовался всеми видами мозаик — регулярными и нерегулярными ( нерегулярные мозаики образуют неповторяющиеся узоры ) — а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.
Сегодня, вы не ученики 6 класса, а творческая мастерская дизайнеров. И перед нами ставится задача создать оригинальный паркет, значит будем использовать ТРИЗ — технологии. Вспомним, что это такое. Приложение 1
- Постановка задачи
- Поиск подобной задачи в базе стандартных задач
- Разбиение поставленной задачи на стандартные
- Решение данной задачи посредством решения стандартных задач, на которые она разбита
- Внесение решенной задачи в базу стандартных задач
— Итак, задача поставлена. Встречалась ли нам до этого момента такая задача, можем ли мы ее назвать стандартной?
— Значит, приступаем ко второму этапу: разбиваем задачу на стандартные задачи и ищем их решение в банке стандартных задач.
- Нужно выбрать элемент паркета и создать его.
Посмотрим, как это делается. Приложение 2
Попробуем разобраться, как Эшер создавал свои орнаменты, на примере паркета с ящерицами. За основу берется фигура, из которой можно составить паркет – правильный шестиугольник. Если «кусочек» плоскости вырезается из внутренней области этого шестиугольника, то такой же надо добавить снаружи.
Мы уже научились производить построения на клетчатой бумаге еще в 5 классе.
2. Заполнить этим элементом всю плоскость.
Как же это сделать? Есть ли такая задача в банке стандартных задач? Вспомним то, что мы изучали о координатной плоскости.
На рисунке показан паркет, т. е. заполнение всей плоскости одинаковыми (равными) фигурами. Как вы думаете, каким образом была заполнена часть плоскости? Что мы можем сделать с данным элементом? Зафиксируем точку с координатой (4;5) и подумаем, в какие точки она может перейти. Напишите координаты точек, в которые может перейти данная точка.
ОГЭ. Задания 1-5. Как решать. Задача про квартиру. Ященко.
Как вы думаете, есть ли какая-нибудь закономерность в изменении абсциссы точки? А ординаты? Давайте запишем это.
Проверим, выполняется ли данное условие для других точек фигуры. Зафиксируем точку B(3;1) и определим координаты точек, в которые она перейдет.
А как вы думаете, сохраняется ли при данном преобразовании расстояние между точками? Проверим.
А что называется расстоянием между точками? Найдем расстояние между точками А и В, А 1 и В 1, А 2 и В 2
Так вот, ребята, преобразование, при котором некоторая точка отображается в другую точку, находящуюся на некотором расстоянии и при этом сохраняется расстояние между точками, называется параллельным переносом.
Параллельным переносом мы будем в дальнейшем пользоваться при построении различных графиков функций в старших классах.
Мы заполнили целую полосу. А что же дальше?
Переходим к следующему этапу: вносим эту задачу, решенную с использованием координатного метода, в базу стандартных задач.
А сейчас, мы, вооруженные новыми знаниями, приступим к работе.
Работа в группах. Заполните плоскость фигурами и запишите, используя лист результатов Приложение 4 , в какие точки при параллельном переносе переходят вершины фигур.
Фигура 1 Фигура 2 Фигура 3
Как же заполнить плоскость без промежутков данными фигурами? Можно, конечно, попробовать разные способы, но тогда потребуется очень много времени. Попробуем систематизировать и рационализировать нашу работу.
При создании элемента паркета мы пользовались определенным свойством. Попробуем использовать его и сейчас. Найдем на элементе выступающую часть и такую же по размеру и форме часть «вырезанную» из внутренней области. Попробуем «приложить» фигуры. Не осталось ли незаполненных областей? Если нет, то продолжаем заполнение полосы.
Заполнив полосу, можем параллельно перенести каждую точку этой полосы. Таким образом, мы заполним всю плоскость.
III. Подведение итогов.
Дидактическая задача этапа
Условия получения положительного результата
Подведение итогов урока . Анализ успешности овладения знаниями и способами деятельности; показать типичные недостатки в знаниях, умениях, навыках
Умение быстро схватывать типичное в успешности усвоения и недостатков, умение учесть реальные учебные возможности
Все знания, полученные на нашем уроке, вам будут необходимы в дальнейшем. Я надеюсь, что вы не утратили интереса, а, напротив, будете стремиться к знаниям более глубоким и не только на уроках математики, но и на других уроках, чтобы войти во взрослую жизнь грамотными и активными
IV. Домашнее задание:
- Подумать, каким образом можно заполнить плоскость паркетом
- Придумать и нарисовать свой паркет.
Источник: nsportal.ru
Внеклассное мероприятие по математике «Геометрический паркет», 7-11 классы
Внеклассное мероприятие по математике «Геометрический паркет» подходит для обучающихся 7-11 классов.
Олимпиады: Математика 1 — 11 классы
Содержимое разработки
4. СОБРАТЬ ПАРКЕТ ПО СХЕМЕ

3. СОБРАТЬ ПАРКЕТ ПО СХЕМЕ
2. СОБРАТЬ ПАРКЕТ ПО СХЕМЕ
1. СОБРАТЬ ПАРКЕТ ПО СХЕМЕ
Содержимое разработки
(Ф. И. обучающегося)
15 марта 2021 г.
1. Построить серединный перпендикуляр
2. Построить правильный пятиугольник
3. Построить правильный шестиугольник
4. Построить правильный треугольник
Содержимое разработки
Внеклассное мероприятие по математике
«Геометрический паркет»
Классы: 7-11.
Цель: определить какие основные геометрические фигуры используются при составлении геометрического паркета и какие виды паркета бывают.
Паркеты с древних времен привлекали к себе внимание людей. Паркеты являются своеобразными орнаментами. Над их созданием трудились многие поколения мастеров, подчас создавая истинные шедевры красоты.
? Что такое геометрический паркет?
Паркет (или мозаика) — бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий.
Паркет — натуральное деревянное напольное покрытие.
Зарождением паркета мир обязан готической Европе, где в тот период (в конце XIII — начале XIV столетий) в домах вельможной знати полы стали выстилаться оригинально подобранными дощечками из различных пород деревьев, которые формировали невообразимо красивые на то время напольные покрытия в форме рисунков и орнаментов.
Паркет (замощение) — специальный случай орнамента.
1 задание
В конвертах находятся комплекты геометрического паркета, которые необходимо собрать.
(музыкальный фон)
? Как вы считаете, выложенную плитку, можно звать паркетом?
Человек, который профессионально кладёт плитку , называется плиточником или облицовщиком.
? А как называют человека, который выкладывает паркет?
Паркетчик — это строительный рабочий, который специализируется на выполнении работ по устройству паркетных полов, подготовке оснований полов под различные виды покрытий.
Итак, давайте посмотрим, на работы наших мастеров — паркетчиков и определим виды этих паркетов.
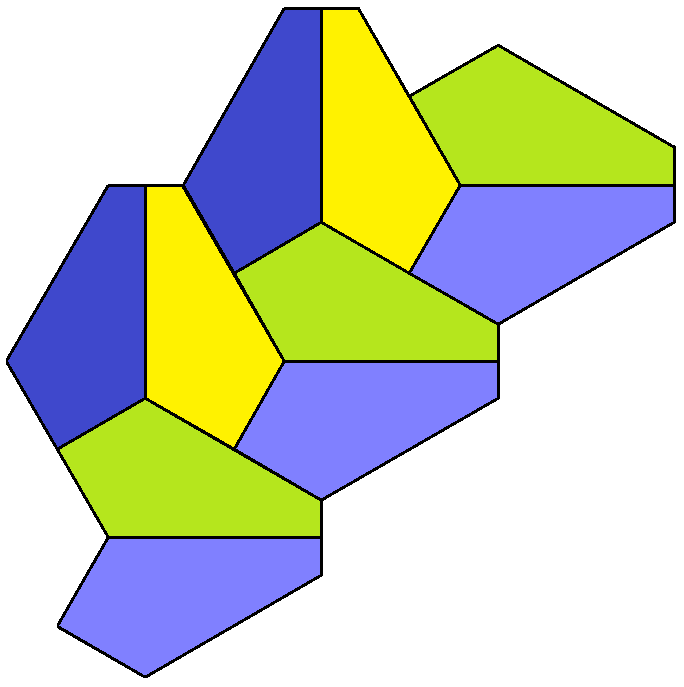
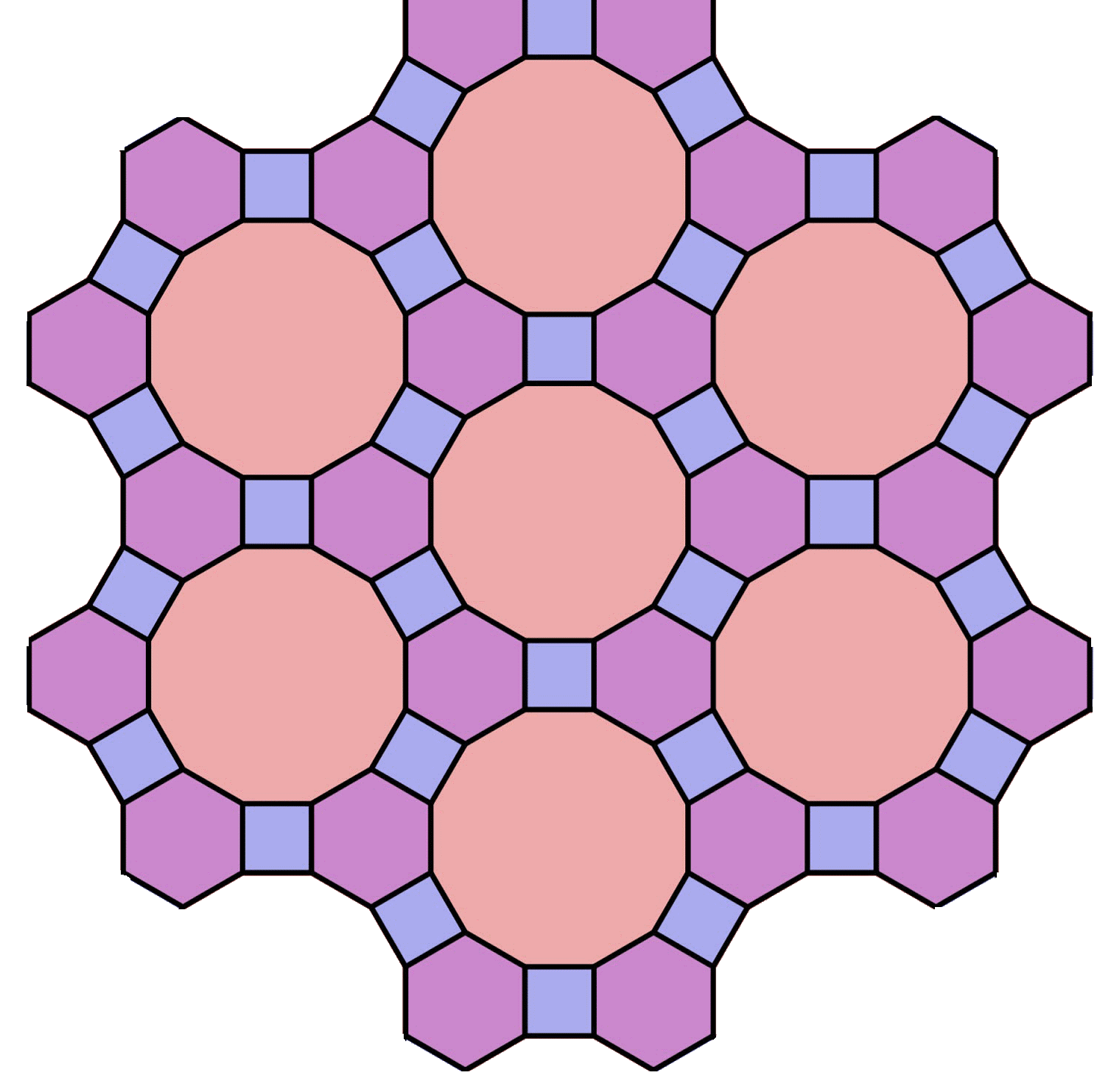
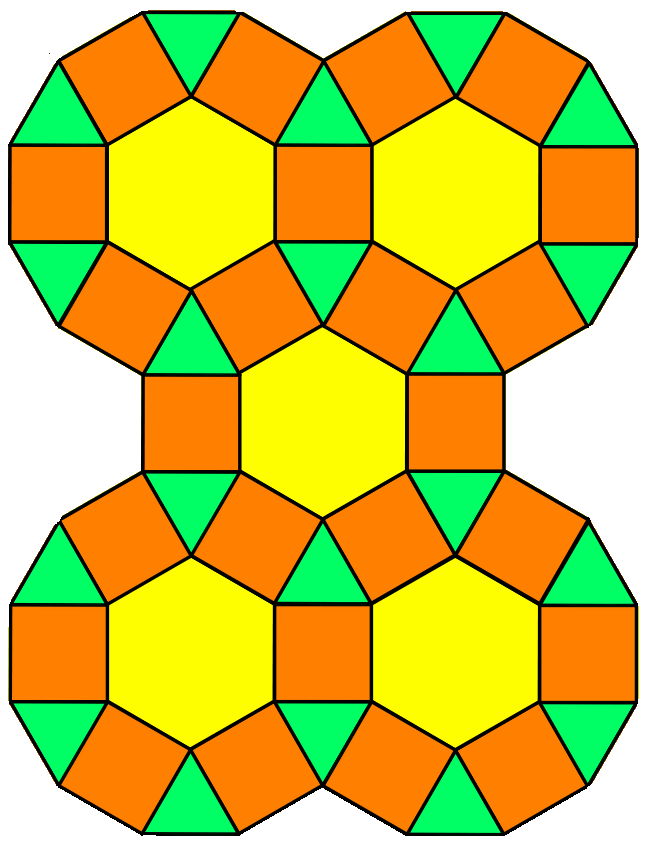
Паркеты бывают правильными, полуправильными и неправильными.
В математике задача сплошного заполнения плоскости многоугольниками без пробелов и перекрытий называется паркетами . Еще древним грекам было известно, что эта задача легко решается при покрытии плоскости правильными треугольниками, квадратами и шестиугольниками, речь идет о правильном паркете, но мы сегодня будем говорить о всех видах паркета с точки зрения математики.
Иногда паркетом называют покрытие, замощение плоскости многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек.
Приведите, пожалуйста, примеры паркета, с которыми вы сталкивались в своей жизни.
? Укладка кафеля, является паркетом?
Керамический паркет – разновидность напольной плитки с оригинальным дизайном. Рельеф и рисунок поверхности повторяют натуральную древесину. Невозможно найти отличия керамического паркета от стандартного деревянного.
В последнее время, широко применяется машинная и ручная паркетная укладка тротуарной плитки.
? Рисунок футбольного мяча, является паркетом?
Геометрический паркет встречается не только на плоскости. Примером паркета на поверхности сферы может являться обычный футбольный мяч. Паркет состоит из 12 пятиугольников и 20 шестиугольников.
? Что такое тесселяция?
Тесселяция — разбиение поверхности на повторяющийся узор геометрических фигур. Тесселяция (греч. tessere, «четырехугольник») – был знаком мастерам многих древних культур, от арабской до индийской и китайской.
Сегодня тесселяция используется в видеоиграх, позволяя создавать детализированную компьютерную графику. Ну а математики такие структуры по замощению поверхностей без промежутков называют просто паркетами.
В последнее время использование мотивов различных паркетов в одежде, аксессуарах, дизайне жилища, строительстве зданий является последним «писком» моды. Математическая теория паркетов имеет свое практическое применение: знание её основ будет полезно дизайнерам, строителям и ремесленникам.
С паркетами мы встречаемся в повседневной жизни. Самым простейшим паркетом является тетрадный лист в клеточку, элементом паркета здесь является квадрат.
Можно придумать сотни, тысячи разных элементов паркета, но нельзя обойтись без знаний геометрии.
У вас у всех лежат брошюры «Геометрический паркет» с геометрическими заданиями, которые мы с вами выполнить, чтобы построить геометрические паркеты:
1. Построить серединный перпендикуляр.
2. Построить правильный пятиугольник.
3. Построить правильный пятиугольник.
4. Построить правильный треугольник.
Паркет широко используется в рукоделии, например, резьба по дереву (таблица значений тригонометрических функций);
в лоскутном шитье — пэчворке.
Пэчворк — это техника шитья вещей из лоскутков ткани. Кусочки сначала соединяют в небольшие блоки в виде разных геометрических фигур.
Тема «Геометрические паркеты» актуальна и в наши дни. Паркетами покрывают полы в домах, укра шают стены комнат и зданий .
В последнее время оформлению паркета уделяется все больше внимания в основе создания и укладки паркета всегда лежит плоская геометрическая фигура чаще всего треугольник, квадрат, ромб, прямоугольник и правильные многоугольники.
Каждому из нас хочется, чтобы было не только прочно, но оригинально и красиво, поэтому без многоугольников ни один дизайнер не обойдется, ни один человек, который собирается сделать ремонт.
С паркетами мы встречаемся каждый день, например, обычный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Можно придумать сотни, тысячи разных элементов паркета.
Источник: compedu.ru
Девятиклассники боятся заданий №1-5 ОГЭ по математике. Но так ли они страшны?
Приветствую, сообщество Хакнем! Неумолимо приближается дата сдачи ОГЭ по математике 2020 года. Сегодня порешаем задания №1-5 .
Практика решения этих заданий с девятиклассниками показывает, что они занимают от 30 минут и больше, в зависимости от уровня подготовки ребёнка. Но, как правило, учащиеся боятся этих заданий и пропускают их.
Мой совет — нужно просто взять и порешать все типы этих заданий, на самом деле, они не сложные, и варианты повторяются.
Разберём сегодня задачу на плане (задания взяты с общеобразовательного сайта Сдам ГИА: Решу ОГЭ) .
Задание 1
Прежде чем решать задания, прочитайте внимательно задачу. Разберитесь по плану — где какой объект находится. Все данные из условия запишите себе кратко, это поможет вам в решении заданий №1-5.
Итак, на плане находятся следующие объекты:
- № 1 — торшер;
- № 2 — диван;
- № 3 — кресло;
- № 4 — журнальный столик;
- № 5 — книжный шкаф;
- № 6 — стул;
- № 7 — письменный стол.
Считайте, первое задание решено — выбираем объекты, которые требует таблица из 1 задания.
Ответ: 7241.
Задание 2
Паркетная доска продаётся в упаковках по 26 штук. Сколько упаковок с паркетной доской нужно купить, чтобы покрыть пол в гостиной?
По условию задачи, паркетная доска имеет размер 40×5 см, по сути, решение заключается в том, чтобы найти количество досок паркета , которое потребуется и затем уже узнать, сколько потребуется упаковок.
Найдём площадь комнаты, для этого посчитаем по картинке, сколько клеток занимает вся площадь: 9 × 12 = 108 клеток. При этом площадь каждой клетки 0,4 × 0,4 = 0,16 м.кв.
- Площадь комнаты: 108 × 0,16 = 17,28 м.кв.
Найдём площадь доски (предварительно выразив размеры в м):
Теперь найдем, сколько потребуется всего досок:
Количество упаковок (по 26 шт. в каждой):
Внимание! Так как мы не можем купить неполную упаковку, требуется 34 упаковки.
Ответ: 34.
Задание 3
Найдите площадь той части гостиной, на которой не будет смонтирован электрический подогрев пола. Ответ дайте в м.кв.
Подогрев не будет смонтирован, где стоят: книжный шкаф + кресло + диван, найдём площади части комнаты, где они стоят, аналогично тому, как находили площадь комнаты, посчитав количество клеток.
Книжный шкаф: 7 × 0,16 = 1,12 кв.м.
Кресло: 4 × 0,16 = 0,64 кв.м.
Площадь дивана есть в условии задачи: 1,6 кв.м.
Итого: 1,12 + 0,64 + 1,6 = 3,36 кв.м.
Ответ: 3,36.
Задание 4
Найдите расстояние от журнального столика до стула (расстояние между двумя ближайшими точками по прямой) в метрах.
Расстояние, которое нужно найти обозначено на картинке красной стрелкой.
Рассмотрим прямоугольный треугольник с катетами 3 и 4 (синие).
По теореме Пифагора найдём гипотенузу:
Кстати, это пифагоров треугольник (есть в задании 20 такой вопрос, существует ли такой треугольник со сторонами 3, 4 и 5 — вот это он и есть) .
Ну и само расстояние будет равно: 5 × 0,4 = 2 м (0,4 м — это длина клетки в м).
Ответ: 2.
Задание 5
В гостиной предполагалось класть ламинат, но решили не экономить и покрыть пол паркетной доской. Ламинат и паркетная доска продаются только в упаковках. Каждая упаковка содержит одинаковое количество м.кв. материала. Сколько рублей можно было бы сэкономить, если бы владелец решил покрыть пол ламинатом?
Для решения этой задачи нужно найти, сколько будет стоить пол, покрытый ламинатом и паркетной доской, и найти разницу.
Как видно, в таблице указана стоимость материала и укладки на 0,16 м.кв., а это, как мы помним, площадь одной клетки на плане. Вся комната у нас (из 1 задания) составляет 108 клеток, поэтому всё просто.
- 108 × 1400 + 108 × 500 = 205 200 руб. (стоимость покрытия паркетной доской);
- 108 × 440 + 108 × 160 = 64 800 руб. (стоимость покрытия ламинатом).
Покрытие ламинатом дешевле на 205 200 – 64 800 = 140 400 руб.
Ответ: 140 400.
Как видите, не такие они сложные, даже совсем не сложные, а будете решать во второй раз, вообще не составят труда. Надеюсь, моя статья поможет вам в подготовке к экзамену! Удачи!
#хакнем_математика ( подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике
Автор : #ирина_чудневцева 42 года, город Ярославль, мама 16-летнего подростка.
Похожие материалы:
- Большинство школьников не решают задачи про ОСАГО в ОГЭ, Разберём, что в них сложного
- Те самые задачи № 1 — 5 ОГЭ по математике с Шинами, которые приводят в ужас девятиклассников
- Такие ли они трудные — задачи на «последовательности» из ОГЭ?
Источник: dzen.ru