Паркет можно составить из любого многоугольника с нечетным числом сторон

Уже пифагорейцам было известно, что име­ется только три вида правильных многоуголь­ников, которыми можно полностью замостить плоскость без пробелов и перекрытий, — тре­угольник, квадрат и шестиугольник (рис. 1). В каждом из этих замощений любые два мно­гоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек.

Паркетом будем называть такое покрытие плоскости правильными многоугольниками, при котором имеют либо общую сторону, либо Общую вершину или совсем не имеют общих точек. Паркет производит приятное впечатление, если он достаточно симметричен. Фигура называется симметричной, если ее можно наложить на саму себя «не правильным» способом (т. е. не таким, когда все точки останутся на своем месте).

Паркеты из правильных многоугольников сами правильные в том смысле, что они «оди­наково устроены» относительно всех своих вершин и всех составляющих паркеты кусоч­ков-многоугольников. (Эти кусочки называ­ются гранями замощения или просто плитка­ми.) Другими словами, для любых двух вершин правильного паркета можно указать такое его самосовмещение, при котором одна из вершин попадает на другую. То же верно для любых двух плиток паркета.

ОГЭ по математике 2020, статград октябрь, задания 1-26

а) б) в)

Паркет называется правильным, если его можно наложить на самого

себя так, что любая заданная его вершин наложится на любую другую

заданную его вершину.

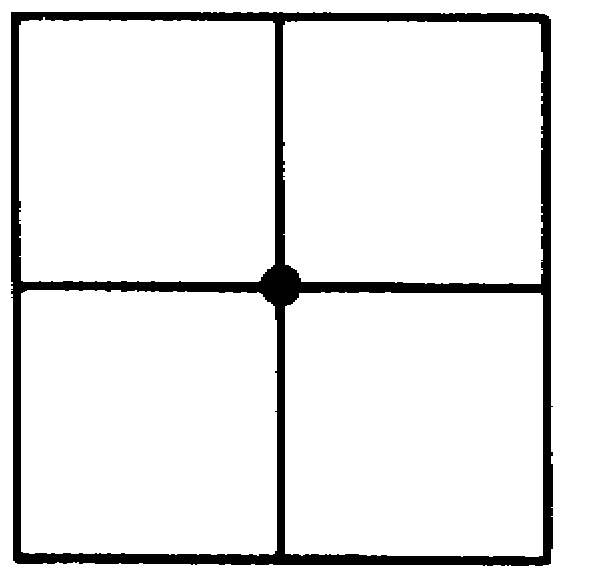
Самый простой из «правильных» паркетов — это разбиение плоскости на квадраты (рис. 1,б). Интересно вы­яснить, сколько есть еще пар­кетов, у которых к каждой вершине паркета примыкают четыре правильных мно­гоугольника и все вершины устроены одинаково (последнее означает, что паркет можно сдвинуть так, что любая его заданная вершина перейдет в любую другую заданную вершину, и все линии совпадут). Это — впол­не практическая задача.

Мы знаем, что сумма углов пра­вильного n-угольника равна 180°(n — 2), а его один угол равен

Пусть в вершине паркета сходятся углы четырех правильных много­угольников: p-угольника, q-угольника, r-угольника и s-угольника. Сумма этих четырех углов должна равняться 360°. Запишем это условие:

Это равенство приводит к соотношению

Если считать, что , то, перебрав все возможности, убеждаемся в том, что существует 14 различных четверок (p, q, r, s). Вот они:

(2, 3, 7, 42); (2, 3, 8, 24); (2, 3, 9, 18); (2, 3, 9, 15); (2, 3, 15, 15);

(2, 4, 5, 20); (2, 4, 6, 12); (2, 4, 8, 8); (2, 5, 5, 10); (2, 6, 6, 6);

(3, 3, 4, 12); (3, 3, 6, 6); (3, 4, 4, 6); (4, 4, 4, 4).

Так как речь идет о много­угольниках, надо отбросить те четвер­ки, где р = 2. Останутся четыре чет­верки: (4, 4, 4, 4); (3, 4, 4, 6); (3, 3, 6, 6); (3, 3, 4, 12).

Первая четверка соответствует пар­кету из одинаковых квадратов (к каждой вершине примыкают 4 пра­вильных четырехугольника — см. рисунок 2).

ЧГК: Что? Где? Когда? математиков на самоизоляции | Fless #matholation

Вторая четверка (3,4,4,6) представ­ляет две возможности для устройст­ва вершины (рис. 3, а, б), но до пра­вильного паркета удается достроить только паркет на рисунке 3, а — по­лучается рисунок 3, в.

в)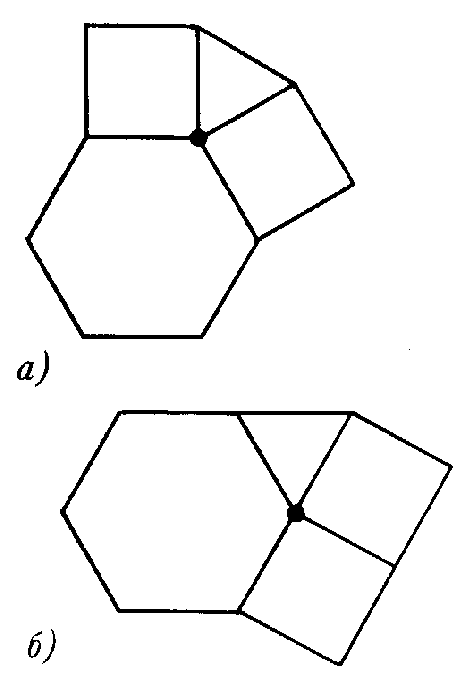

Третьей четверке (3,3,6,6) также со­ответствуют два расположения многоугольников в вершине (рис. 4, а, б), и только второй случай, изображен­ный на рисунке 4, б, достраивается до правильного паркета (рис. 4, в)

а) 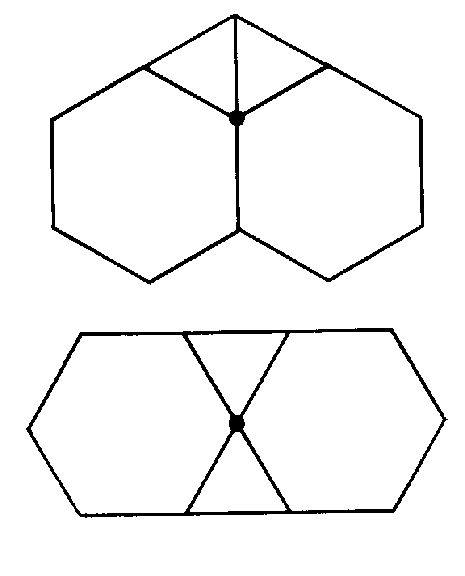в)

Два рисунка (рис. 5, а, б), соот­ветствующих четвертой четверке (3,3, 4,12), до правильного паркета не до­страиваются.

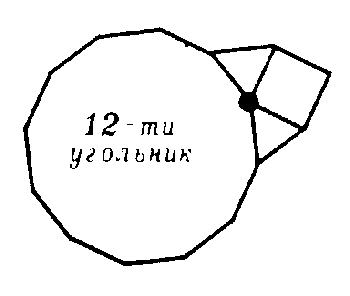
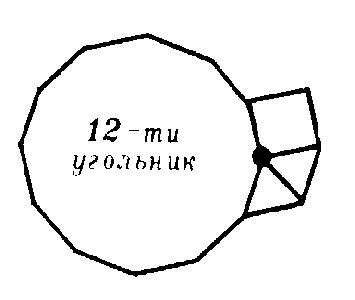
Сколько всего правильных парке­тов? Как они устроены? Наша зада­ча — ответить на эти вопросы.

Легко видеть, что вообще парке­тов — не обязательно правильных — существует бесчисленное множество (Два паркета мы считаем различ­ными, если не существует гомотетии плос­кости, переводящей один из этих паркетов в другой.). Од­нако, подобно тому как при бесчис­ленном множестве многогранников вообще существует лишь конечное число правильных многогранников, так и при бесчисленном множестве паркетов существует лишь конечное число правильных паркетов.

Решение нашей задачи естествен­но начать с исследования вершин паркета. Из определения правильно­сти сразу вытекает принцип эквивалентности вер­шин: любые две вершины устроены одинаково в том смысле, что звезды всех вершин одинаковы. (Звездой вершины называется фигура, обра­зованная всеми многоугольниками, содержащими ее.)

Обозначим через число приле­гающих к вершине i-угольников, а че­рез ai — величину внутреннего угла правильного i-угольника. Тогда в каждой вершине, очевидно, выпол­няется соотношение.

где в сумму мы включаем все слагае­мые с номерами i, для которых к вер­шине примыкает хотя бы один i-угольник.

Подставляя в эту формулу извест­ное из геометрии выражение для ai,

ai =2(1 – )d, и сокращая на 2d, получим

Таким образом, числа являются целочисленными решениями уравнения (1) . Однако, как мы увидим ниже, не все целочисленные решения уравнения (1) реализуются правильными паркетами!

Далее, в вершине паркета может сходиться не более шести и не менее трех многоугольников. Действительно, при схождении в одной вершине семи или более многоугольников хотя бы один угол в правильном многоугольнике должен быть менее , что невозможно (минимальный, угол — у треугольника — равен). При схождении в одной вершине двух многоугольников у одного из них внутренний угол должен быть более 2d (180°), что, очевидно, также невозможно. Таким образом, реше­ние задачи распадается на анализ тех вариантов, когда в вершине паркета сходятся 3, 4, 5 и 6 правиль­ных многоугольников.

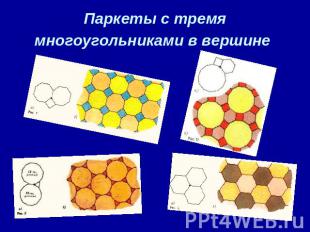
Паркеты с тремя многоугольниками в вершине

Здесь, в свою очередь, в принципе возможны три случая (в зависимости от набора многоугольников в каждой вершине):

1°. Три одинаковых многоуголь­ника.

2°. Два одинаковых и один отлич­ный от них.

3°. Три различных многоуголь­ника.

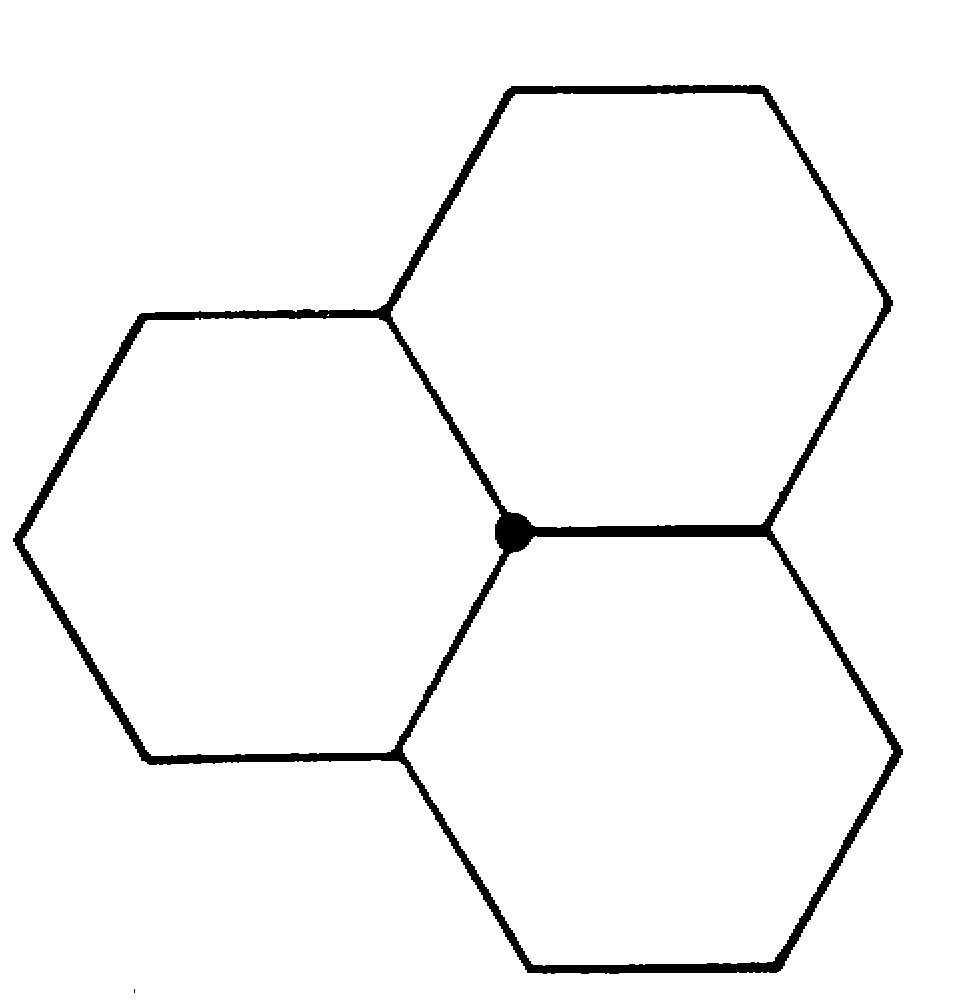
В первом случае сумма в уравне­нии (1) сводится к одному слагаемо­му, отвечающему трем одина­ковым n-угольникам, поэтому мы

получаем или п = 6,

то есть к каждой вершине примыкает 3 шестиугольника. Это один из про­стейших правильных паркетов (рис.6).

Для второго случая (два k-угольника, один n-угольник) имеем

Целочисленные решения последнего уравнения проще всего найти

перебором различных значений:

Продолжать перебор дальше нет смыс­ла, так как целочисленных k мы больше не получим: ,

а при n >10 последнее слагаемое не может быть целым.

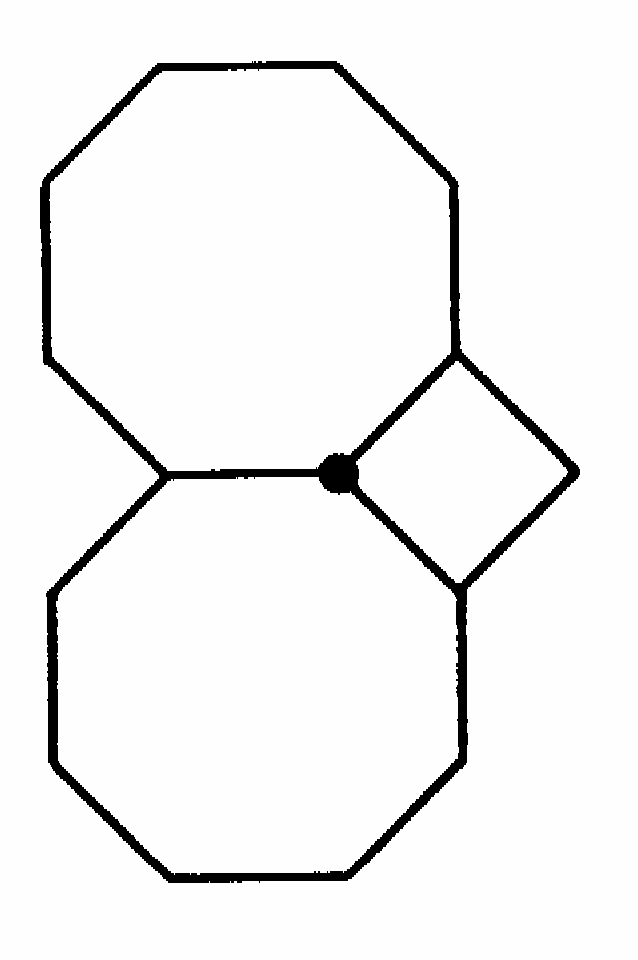
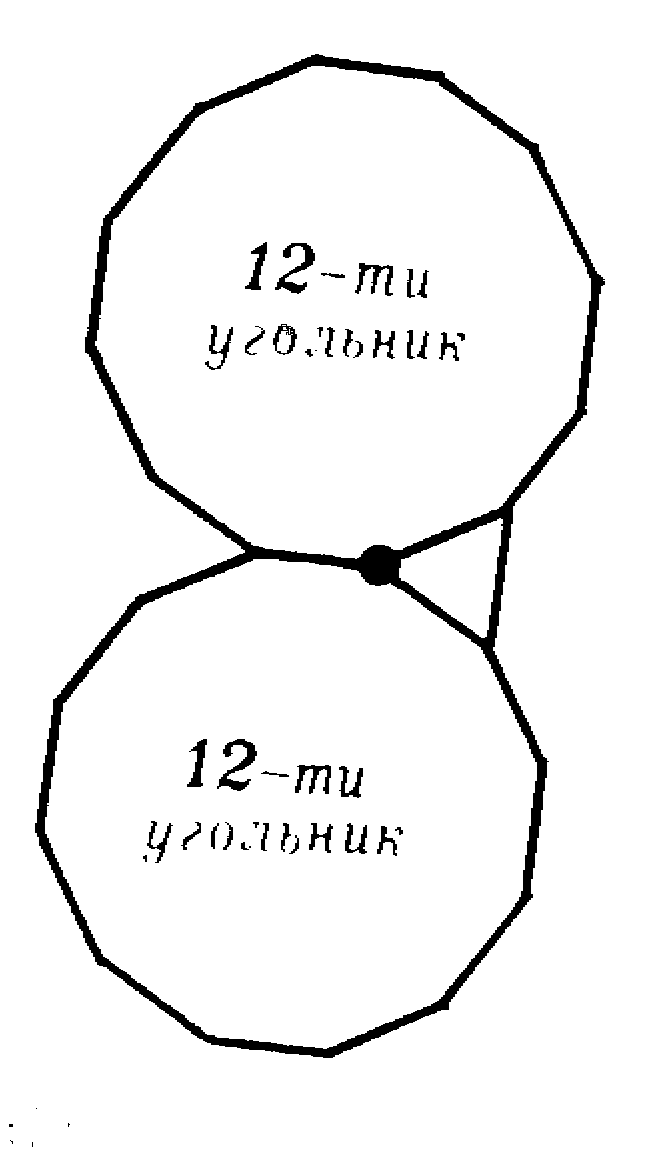
Таким образом, кроме уже рас­смотренного случая n= k = 6 мы получили три решения, которые мы запишем в виде суммы углов в вершине:

Первому решению отвечает пар­кет, часто встречающийся на прак­тике (рис. 7).

Менее обычный паркет, отвечающий второму решению, изо­бражен на рисунке 8.

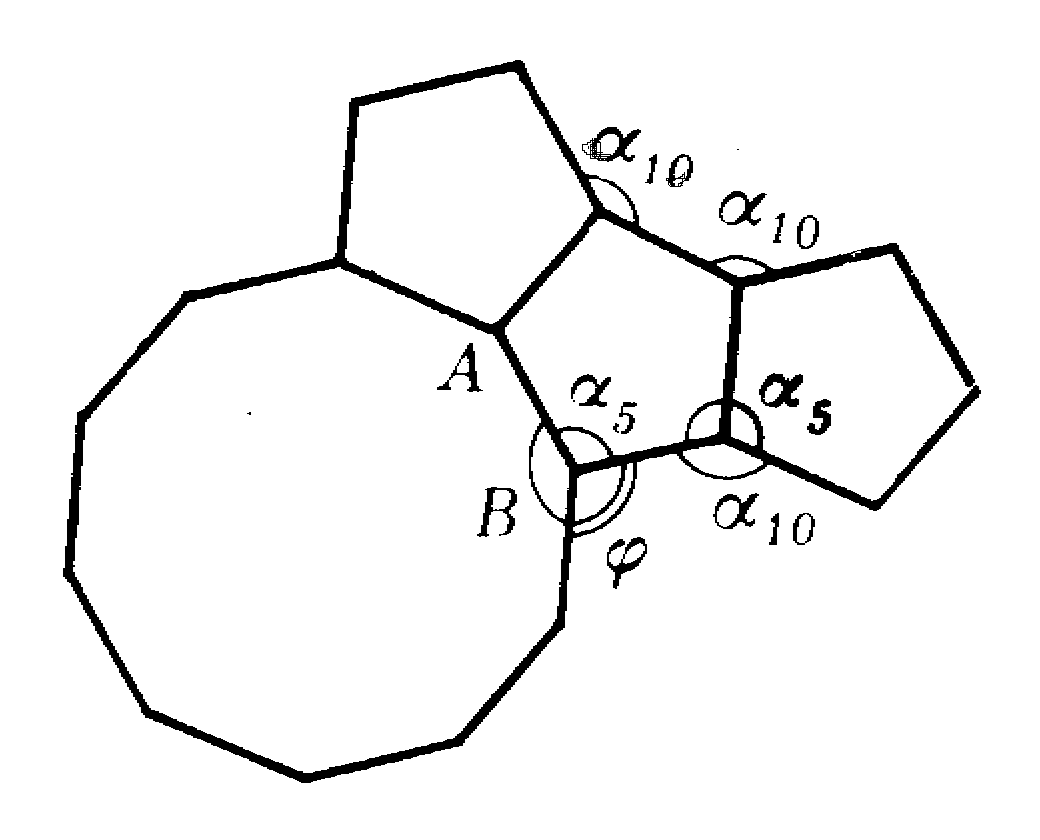
А вот комбинация , в отличие от ранее рассмотренных, пра­вильного паркета не образует. Убе­диться

в этом позволяет «достройка» (рис.9) окружения вершины А еще одним многоугольником. Из нее видно, что один из углов при вершине В (угол, обозна­ченный на рисунке 10 через ), по принципу эквивалентности вершин, должен быть равен . На самом же деле, угол равен . Рис. 9

Правильного паркета типа не сущест­вует.

Для оставшегося, наиболее слож­ного, третьего случая (три разных многоугольника с n, т и k вершина­ми) уравнение (1) приводится к виду

Чтобы не разбирать всех возможных числовых решений, нам будет нужна следующая

Лемма. В вершине правильного паркета не могут сходиться три раз­личных многоугольника, у одного из которых нечетное число сторон.

Действительно, пусть такой пар­кет существует (рис. 10). Тогда вок­руг нечетноугольника оставшиеся т- и n-угольники должны идти че­редуясь. Поэтому при его обходе ря­дом окажутся два одинаковых мно­гоугольника, вопреки условию лем­мы.

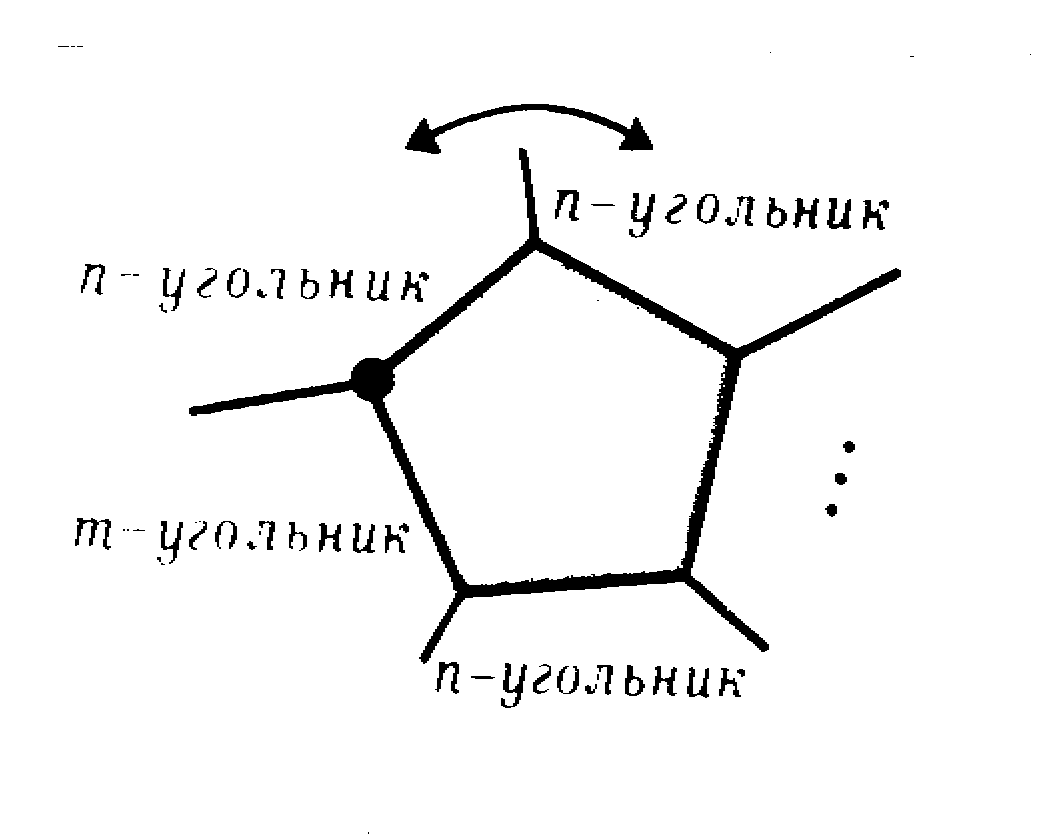
Благодаря лемме мы можем в (2) заменить k на 2k, т на 2т,l на 211 и перейти к уравнению

Не нарушая общности, можно пред­положить, что k1

Источник: geum.ru

Паркет можно составить из любого многоугольника с нечетным числом сторон

Если в одной вершине паркета сходится m правильных n — угольников, то должно выполняться равенство откуда

Возможными допустимыми значениями n являются 3, 4 и 6. При остальных значениях n число m оказывается дробным. В частности, нельзя заполнить плоскость правильными пятиугольниками.
Расширим способы составления паркетов из правильных многоугольников, разрешив использовать в них правильные многоугольники с различным числом сторон.
Обозначим через a 1 , a 2 , … углы правильных многоугольников, имеющих общую вершину. Расположим их в порядке возрастания. Учитывая, что сумма всех таких углов должна быть равна 360 ° , составим таблицу, содержащую возможные наборы углов и укажем соответствующие паркеты.

a 1	a 2	a 3	a 4	a 5	a 6	a 1 + a 2 +…=360 °
60 °	60 °	60 °	60 °	60 °	60 °	Паркет из 3-ов (рис. 2)
60 °	60 °	60 °	60 °	120 °	Паркет из 3-ов и 6-ов (рис. 4)
60 °	60 °	60 °	90 °	90 °	Два паркета из 3-в и 4-в (рис. 5 , 6)
60 °	60 °	90 °	150 °	Нет паркета
60 °	60 °	120 °	120 °	Паркет из 3-в и 6-в (рис. 7)
60 °	90 °	90 °	120 °	Паркет из 3-в, 4-в и 6-в (рис. 8)
60 °	150 °	150 °	Паркет из 3-в и 12-в (рис. 9)
90 °	90 °	90 °	90 °	Паркет из квадратов (рис. 1)
90 °	120 °	150 °	Паркет из 4-в, 6-в и 12-в (рис. 10)
90 °	135 °	135 °	Паркет из 4-в и 8-в (рис. 11)
120 °	120 °	120 °	Паркет из 6-ов (рис. 3)

Таким образом, всего имеется 11 типов правильных паркетов.
Рассмотрим теперь вопрос о заполнении плоскости неправильными равными многоугольниками.
Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.
Доказательство. Пусть дан четырехугольник АВС D (рис. 12). Рассмотрим центрально симметричный ему четырехугольник относительно середины стороны АВ. Исходный четырехугольник АВСD обозначим цифрой 1, а симметричный — цифрой 2. Теперь четырехугольник 2 отразим симметрично относительно середины его стороны ВС.

Полученный четырехугольник обозначим цифрой 3 и отразим его симметрично относительно середины его стороны CD . Полученный четырехугольник обозначим цифрой 4. Четырехугольники 1, 2, 3 и 4 примыкают к общей вершине углами А, В, С и D . А так как сумма углов четырехугольника равна 360 ° , то эти четырехугольники заполнят часть плоскости вокруг общей вершины. Такое же построение можно провести вокруг каждой новой вершины, что и даст искомое заполнение плоскости. Заметим, что четырехугольники, закрашенные одним цветом (рис. 12), получаются друг из друга параллельным переносом.
Заполнение плоскости может быть произведено не только многоугольниками, но и фигурами более сложного вида. Повторяющиеся равные фигуры являются основой составления орнаментов, с давних времен привлекавших к себе внимание людей. Знаменитый голландский художник Мариус Эшер (1898-1972) посвятил орнаментам несколько своих картин. Среди них: «Всадники» (рис. 13), «Летящие птицы» (рис.

14); «Ящерицы» (рис. 15).

Рис. 13

Литература
1. Кокстер Г.С.М. Введение в геометрию. – М.- Наука, 1966, с. 100.
2. Васильев Н.Б. и др. Математические соревнования. Геометрия. – М.: Наука, 1974, с.15 /Библиотечка физико-математической школы, выпуск 4.
3. Доморяд А.П. Математические игры и развлечения. – М.; 1961.
5. Заславский А. Паркеты и разрезания //Квант. – 1999. — № 2. – С.32.
6. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
7. Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе “Paint” //Математика в школе. – 2000. — № 8. – С.54.
8. Журнал //Квант. 1979. — № 2. – С.9; 1980. — № 2. – С.25; 1986. — № 8. – С.3; 1987. — № 6. – С.27; 1987. — № 11. – С.21; 1989. — № 11. – С.57.
9. Журнал //Математика в школе. 1967. — № 3. – С.75; 1986. № 1. – С.59;

Источник: vasmirnov.ru

Презентация на тему: Геометрические паркеты (9 класс)

Описание слайда:

№ слайда 2

Описание слайда:

Цель:подробно изучить паркеты.

№ слайда 3

Описание слайда:

Задачи: 1. Изучить литературу о паркетах. 2. Найти исторический материал. 3. Научиться решать задачи.

№ слайда 4

Описание слайда:

Гипотеза: количество правильных паркетов бесчисленное множество.

№ слайда 5

Описание слайда:

Что такое паркет? Паркет — это такое покрытие плоскости многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек.

№ слайда 6

Описание слайда:

№ слайда 7

Описание слайда:

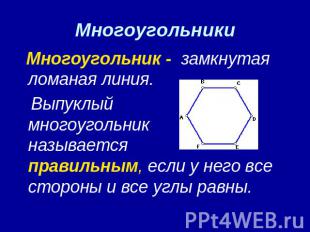
Многоугольники Многоугольник — замкнутая ломаная линия. Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.

№ слайда 8

Описание слайда:

Полуправильные многоугольники I) Выпуклый многоугольник с четным числом вершин называется равноугольно-полуправильным, если его стороны, взятые через одну, равны и все его углы равны. II) Выпуклый многоугольник с четным числом вершин называется равносторонне-полуправильным, если его углы, взятые через один, равны и все его стороны равны.

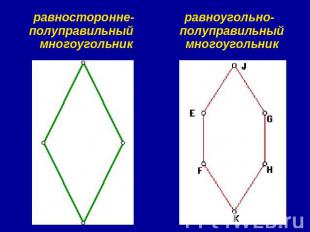
№ слайда 9

Описание слайда:

равносторонне-полуправильный многоугольник равноугольно-полуправильный многоугольник

№ слайда 10

Описание слайда:

№ слайда 11

Описание слайда:

Правильные паркеты Паркет называется правильным, если он составлен из правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом.

№ слайда 12

Описание слайда:

№ слайда 13

Описание слайда:

Паркеты с тремя многоугольниками в вершине

№ слайда 14

Описание слайда:

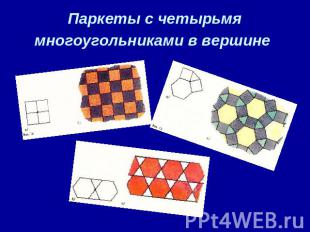
Паркеты с четырьмя многоугольниками в вершине

№ слайда 15

Описание слайда:

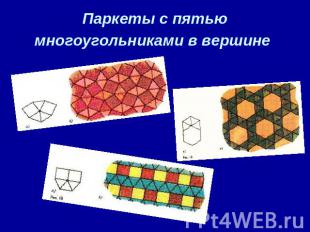
Паркеты с пятью многоугольниками в вершине

№ слайда 16

Описание слайда:

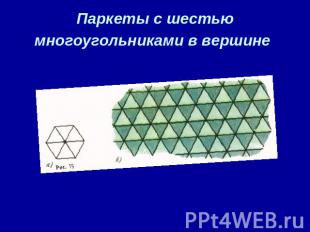
Паркеты с шестью многоугольниками в вершине

№ слайда 17

Описание слайда:

Паркеты из неправильных многоугольников Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:

№ слайда 18

Описание слайда:

Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма. Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами.

№ слайда 19

Описание слайда:

Паркеты из произвольных фигур

№ слайда 20

Описание слайда:

Задачи Докажите, что для любого четырехугольника существует паркет, состоящий из четырехугольников равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.

№ слайда 21

Описание слайда:

Я считаю, что цель моей работы достигнута. Выдвинутая мною гипотеза о бесконечном множестве правильных паркетов оказалась неверна: в ходе работы я выяснила, что правильных паркетов только 11.

№ слайда 22

Описание слайда:

1. Васильев Н.Б. и др. Математические соревнования. Геометрия. — М.: Наука, 1974, с. 15 /Библиотечка физико-математической школы, выпуск 4.2. Доморяд А.П. Математические игры и развлечения. — М.; 1961.3. Журнал //Квант. 1979. — № 2. — С.9; 1980. — № 2. — С.25; 1986 — № 8 — С 3* 1987. — № 6. — С.27; 1987. — № 11. — С.21; 1989. — № 11. — С.57.4.

Журнал //Математика в школе. 1967. – № 3. – С.75; 1986. № 1. – С.59;5. Заславский А. Паркеты и разрезания //Квант. — 1999. — № 2. — С.32.6. Кокстер Г.С.М. Введение в геометрию. — М.- Наука, 1966, с. 100.7. Смирнова И.М. В мире многогранников. — М.: Просвещение, 1995.8.

Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе «Paint» //Математика в школе. — 2000. — № 8. — С.54.

№ слайда 23

Источник: ppt4web.ru