320200. На фабрике керамической посуды 10 процентов произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов.
Ответ округлите до сотых.
Число всевозможных и благоприятных исходов явно не задано (так как о количестве тарелок в условии нет информации). а нам необходимо найти отношение количества тарелок без дефектов поступивших в продажу к количеству всех тарелок.
Обозначим за n – это количество тарелок, которые произвёл завод. В продажу поступят все качественные тарелки (это 0,9n) плюс 20% не выявленных дефектных тарелок (это 0,2 от 0,1n), то есть получится 0,9n + 0,2∙0,1n = 0,92n тарелок. Это и есть число всевозможных исходов.
Поскольку качественных из них 0,9n, то это есть число благоприятных исходов, Получается что вероятность купить качественную тарелку будет равна: Округляем до сотых, получим 0,98
Мы просто берём конкретное число тарелок которое произвёл завод, пусть их будет 100.
Получается, что качественных тарелок 90. Не выявленных дефектных тарелок 20% от 10, то есть две. Получаем, что в продажу поступят 90 качественных плюс 2 с дефектами => 92.
Итак,число возможных исходов 92, благоприятных 90. Вычисляем отношение.
Источник: matematikaege.ru
Задачи по теории вероятности
В работе подобраны задачи разного уровня сложности.В настоящее время задачи по теории вероятности в 9 и 11 классах усложняются. Я думаю, учителям понравится подборка задач, которая может применятся на уроках. К сожалению, ученики в школе имеют затруднение при решении задач по теории вероятности А зто интересная тема. Надо бы и в учебниках школьных включать больше задач по этой теме.
Оленич Вера Николаевна
Содержимое разработки
ОДИНЦОВСКИЙ УМЦ «РАЗВИТИЕ ОБРАЗОВАНИЯ»
ЗАЧЁТНАЯ РАБОТА
на тему: «ТЕОРИЯ ВЕРОЯТНОСТЕЙ»
ОЛЕНИЧ ВЕРЫ НИКОЛАЕВНЫ
ГОРЕНИНА ЕЛЕНА ВАЛЕНТИНОВНА
г.Одинцово
2018-2019
1).На заводе керамической плитки 5% произведённых плиток имеют дефект. При контроле качества продукции обнаруживается лишь 40% дефектных плиток. Остальные плитки отправляются на продажу. Найдите вероятность того, что выбранная случайным образом при покупке плитка не будет иметь дефектов.
Ответ округлите до сотых.Скрыть решение
Решение.
При контроле качества продукции выявляется 40% дефектных плиток, которые составляют 5% от произведённых плиток, и они не поступают в продажу. Значит, не поступает в продажу 0,4 · 5% = 2% от произведённых плиток. Остальная часть произведённых плиток — 100% − 2% = 98% поступает в продажу.
Не имеет дефектов 100% − 95% произведённых плиток. Вероятность того, что купленная плитка не имеет дефекта, равна 95% / 98% = 95/98 ≈0,97
2).Вероятность того, что аккумулятор не заряжен, равна 0,15.Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены.
Решение
Вероятность того, что аккумулятор заряжён, равна 1-0,15 = 0,85.1−0,15=0,85.Найдём вероятность события «оба аккумулятора заряжены». Обозначим через A и B события «первый аккумулятор заряжён» и «второй аккумулятор заряжён». Получили P(A) = P(B) = 0,85.P(A)=P(B)=0,85.Событие «оба аккумулятора заряжены» — это пересечение событий A∩B, его вероятность равна P(A∩B)= P(A)⋅P(B)= =0,85⋅0,85= 0,7225.
3)Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 7»?
Решение
Исходом будем считать пару чисел: очки при первом и втором броске. Тогда указанному событию благоприятствуют следующие исходы: 1-6,1−6, 2-5,2−5, 3-4,3−4, 4-3,4−3, 5-2,5−2, 6-1.6−1. Их количество равно 6.
4).На рисунке изображён лабиринт. Жук заползает в лабиринт в точке «Вход». Развернуться и ползти в обратном направлении жук не может, поэтому на каждой развилке он выбирает один из путей, в котором еще не был. С какой вероятностью жук придет к выходу Д, если выбор дальнейшего пути является случайным.
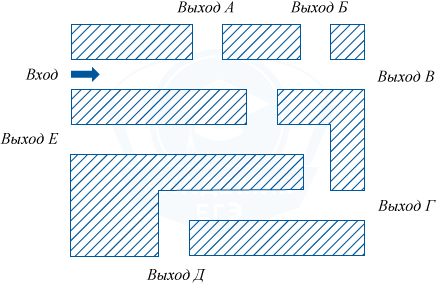
Скрыть решение
Расставим на перекрёстках стрелки в направлениях, по которым может двигаться жук (см. рис.).
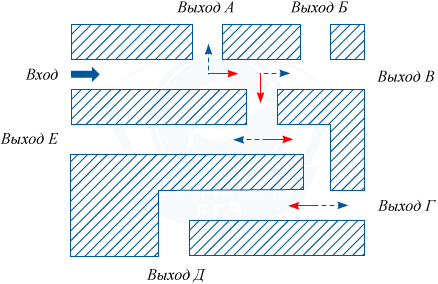
Выберем на каждом из перекрёстков одно направление из двух возможных и будем считать, что при попадании на перекрёсток жук будет двигаться по выбранному нами направлению.
Чтобы жук достиг выхода Д, нужно, чтобы на каждом перекрёстке было выбрано направление, обозначенное сплошной красной линией. Всего выбор направления делается 4 раза, каждый раз независимо от предыдущего выбора. Вероятность того, что каждый раз выбрана сплошная красная стрелка, равна 1/2*1/2*1/2*1/2= 0,0625.
5).Стоянка освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,4. Найдите вероятность того, что за год хотя бы одна лампа не перегорит.
рыть решение
Решение
Сначала найдём вероятность события «обе лампы перегорели в течение года», противоположного событию из условия задачи. Обозначим через A и B события «первая лампа перегорела в течение года» и «вторая лампа перегорела в течение года». По условию P(A) = P(B) = 0,4. Событие «обе лампы перегорели в течение года» — это A∩B, его вероятность равна P(A∩B)= =P(A)⋅P(B) =0,4⋅0,4= 0,16 (так как события A и B независимы).
Искомая вероятность равна 1−P(A∩B) =1−0,16= 0,84.
6).Из города М. в город Р. ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 15 пассажиров, равна 0,64. Вероятность того, что в автобусе окажется меньше 10 пассажиров, равна 0,46. Найдите вероятность того, что в этот день пассажиров будет от 10 до 14.
Скрыть решение
Обозначим через A событие «в автобусе окажется меньше 10 пассажиров» и через B событие «число пассажиров будет от 10 до 14». Они несовместны, и их объединением является событие «в автобусе окажется меньше 15 пассажиров», поэтому сумма вероятностей событий A и B равна вероятности события A∪B, то есть P(A∪B)=P(A)+P(B). Искомая вероятность равна P(B) =0,64−0,46=0,18.
7). Кубик бросили трижды. Найдите вероятность того, что в сумме выпало 12 очков.
Как найти общее количество исходов, мы прописали в примере 1.7: Nобщ=216.
А вот что делать с количеством благоприятных исходов? Можно, конечно, составить полную таблицу, как в предыдущем случае. Но тогда потеря одного из исходов влечет за собой неверный ответ. Давайте поступим немножко по-другому, запишем просто все возможные комбинации цифр от 1 до 6, в сумме дающие 12, не переставляя их местами:
С цифрой 6 закончили.
Теперь внимательно следим за тем, чтобы в дальнейших случаях она случайно не появилась, иначе это будет всего лишь перестановкой уже рассмотренного случая.
Всего получилось 6 комбинаций.
Но ведь мы еще можем переставлять цифры местами в каждой из них! Чтобы не вводить понятия комбинаторики, предлагаю запомнить: Если все 3 цифры разные – они дают 6 комбинаций. Если 2 цифры совпадают, а третья отличается – то 3 комбинации. Если все цифры одинаковые – 1 комбинация.
Используя это правило, найдем количество благоприятных исходов: Nбл=6+6+3+3+6+1=25 Вероятность равна: р = 25/ 216 =0,1157. После первого округления получаем значение р=0,116. После второго – р=0,12.
8). Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнѐт игру с мячом. Команда «Ротор» по очереди играет с командами «Протор», «Стартер» и «Монтѐр». Найдите вероятность того, что «Ротор» будет начинать только первую и вторую игры.
«Ротор» сыграет 3 игры. Вероятность, что жребий будет в пользу «Ротора», равна р=1/ 2 . Тогда вероятность того, что жребий выиграет НЕ «Ротор» равна р=1- 1/ 2 = 1/ 2 . Для того, чтобы выполнились условия задачи, нам необходимо, чтобы «Ротор» начал И первую, И вторую игры, И НЕ начал третью игру. Р = 1 /2 * 1/ 2 *(1- 1/ 2 )= 1/ 8 =0,125
9). Офис закупает канцелярию для сотрудников трех различных фирм. Причем, продукция первой фирмы составляет 40% всех поставок, а остальных двух – поровну. Чаще всего приходится закупать пишущие ручки. Опытным путем выяснилось, что 2% ручек второй фирмы – бракованные.
Процент брака в первой и третьей фирме составляет 1% и 3% соответственно. Сотрудник М. с утра взял ручку из новой поставки канцелярии. Найдите вероятность того, что она будет исправна.
Все аналогичные задачи решаются построением таблицы. Но прежде выполним дополнительные вычисления.
Найдем, сколько процентов от поставок составляет продукция 2 и 3 фирмы.
Источник: videouroki.net
Задача 4 ЕГЭ На фабрике керамической посуды 30 % произведённых тарелок имеют дефект. 50

На фабрике керамической посуды 30 % произведённых тарелок имеют дефект. При контроле качества продукции выявляется 50 % дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
(Ященко 36 вариантов 2023 Задача 4 из Варианта 24)
Из условия задачи следует, что из 30% бракованных тарелок, выявляется только 50%, т.е. 30% · 0,5 = 15% брака от всего объема произведенных тарелок. В продажу поступает 100% — 15% = 85% тарелок и среди них бракованных 30% — 15% = 15%. Таким образом, вероятность того, что случайно выбранная тарелка не будет иметь дефектов, равна

Подписывайтесь, дорогие друзья
Источник: xn--80aerobhh.xn--p1ai