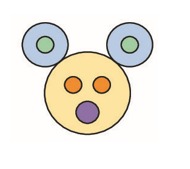
На занятии математического кружка ваня узнал что паркеты которые составлены

1. Сколько кругов изображено на рисунке?

А) 5
Б) 6
В) 7
Г) 8
Д) 9

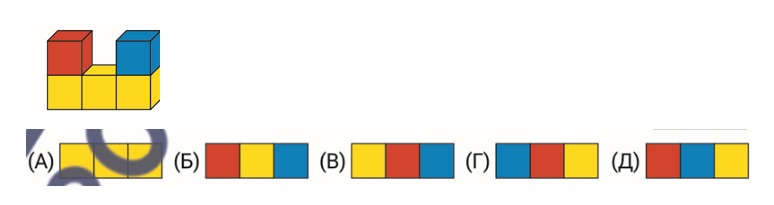
2. Кенгуру построили фигуру из пяти кубиков. Как Выглядит эта фигура, если смотреть на нее сверху?

3. Имеется пять стеклянных ваз. В какой лежат шары с написанными на них номерами. В какой вазе сумма чисел на всех шарах наибольшая?

Ответ: А

4. Миша разрезал квадрат так. как показано на рисунке 1. Из получившихся кусочков он составил фигуру (рисунок 2). Какой из кусочков Миша не использовал, когда составлял фигуру?

Математика и смекалка

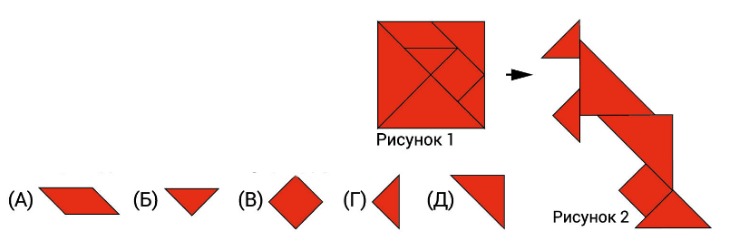
Ответ: А

5. Петя нарисовал кораблик. На его кораблике нарисовано больше одного круга. Треугольников на нём на 2 больше, чем квадратов. Какой из корабликов нарисовал Петя?

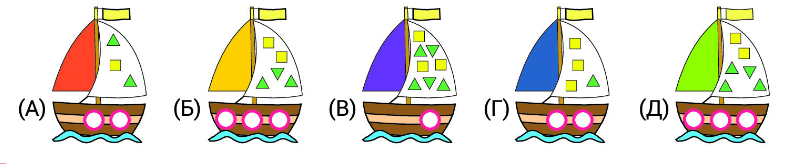
Ответ: Д

6. На каком рисунке фигуры не являются отражением друг друга относительно пунктирной линии?

Ответ: Б

7. У Вани было пять одинаковых свечей. Он зажёг их одновременно, а затем погасил каждую в своё время. После этого свечи стали выглядеть так, как показано на рисунке. Какую свечу Ваня потушил первой?

А) A
Б) B
В) C
Г) D
Д) E

8. В верном равенстве два одинаковых числа были закрыты квадратами со 20+10+10+?+?+1=51 знаками вопроса. Какие числа были закрыты?
А) 1
Б) 2
В) 5
Г) 10
Д) 20

9. Диск с двумя отверстиями накладывают на циферблат часов и вращают вокруг центра. Какую ещё пару чисел можно увидеть одновременно?

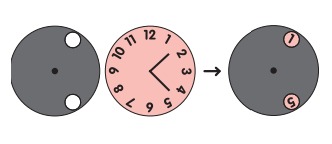
Сериал «Математический кружок», сцена 5

А) 4 и 9
Б) 5 и 9
В) 5 и 10
Г) 6 и 9
Д) 7 и 12

10.У Алисы есть четыре кусочка пазла. Какие два кусочка она должна сложить вместе, чтобы получить полный квадрат?

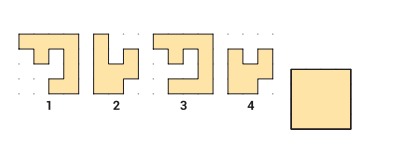
А) 1 и 2
Б) 1 и 3
В) 1 и 4
Г) 2 и 3
Д) 2 и 4

11. Светотехник в театре включает цветные прожекторы по такому плану:

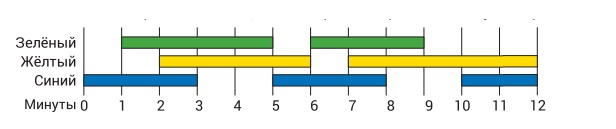
В течение первой минуты светит только синий прожектор. В последние две минуты светят жёлтый и синий прожекторы. Суммарно в течение скольких минут светят ровно два прожектора одновременно?

А) 2 минуты
Б) 6 минут
В) 8 минут
Г) 9 минут
Д)10 минут

5-8 классы

1. Валера заполняет таблицу числами от 1 до 40 подряд, как показано на рисунке. Какой кусочек он сможет вырезать из таблицы, когда заполнит её до конца?

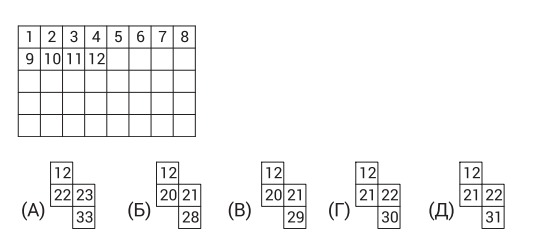
Ответ: В

2.Кенгуру составляет числа из спичек. Цифры от 0 до 9 он всегда составляет так, как показано на рисунке. Например, чтобы составить таким способом число 15 или 8, ему потребуется семь спичек. Какое наибольшее положительное число кенгуру может составить из семи спичек?

А) 31
Б) 51
В) 74
Г) 711
Д) 800

3.У Иры есть развёртка, из которой она складывает кубик. Какой из следующих пяти кубиков у неё получился из этой развёртки?

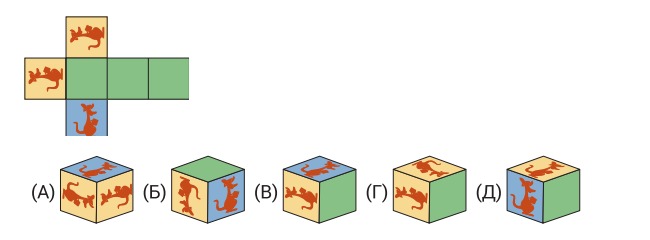
Ответ: Б

4.Альпинист взбирается по цилиндрической башне снизу вверх. Его путь отмечен на рисунке чёрным цветом. Все шаги альпиниста одинакового размера. Девять шагов видны на изображении. Сколько его шагов не видны?

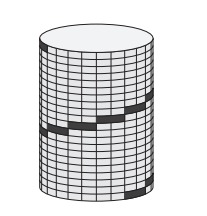
А) 9
Б) 10
В) 11
Г) 12
Д)13

5.У Саши есть пять дисков разных размеров. Он хочет построить такую башню из четырёх дисков, где каждый следующий диск меньше, чем предыдущий. Сколько различных вариантов таких башен Саша может построить?

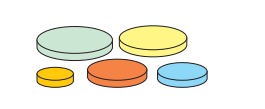
А) 4
Б) 5
В) 9
Г) 12
Д) 20

6.Решётка на рисунке состоит из вертикальных и горизонтальных линий. Одна часть этой решётки была скрыта. Какой из следующих кусочков является скрытой частью решётки?

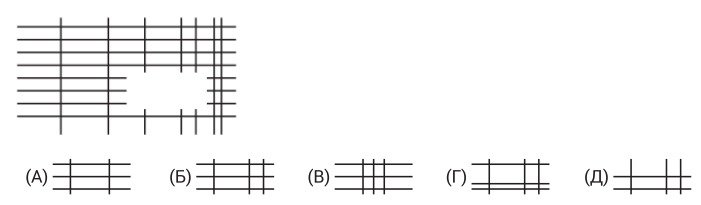
Ответ: Б

7.Какую из следующих фигур нельзя разделить на две трапеции одной прямой линией?

Ответ: А

8. Диск с двумя отверстиями наложен на циферблат часов так, как показано на рисунке. Диск вращают вокруг центра до тех пор, пока в одном из отверстий не появится цифра 8. Какие два других числа возможно увидеть одновременно с ней?

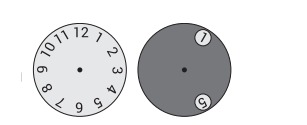
А) 4 или 12
Б) 1 или 5
В) 1 или 4
Г) 7 или 11
Д) 5 или 12

9. Коля хочет расставить по одному числу в каждой вершине ромба так, чтобы число, написанное на ребре, равнялось сумме двух чисел в вершинах, которые это ребро соединяет. Какое число должно стоять на месте вопросительного знака?

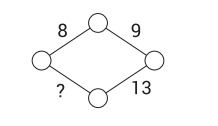
А) 11
Б) 12
В) 13
Г) 14
Д) 15

10.У Кристины есть кусок прозрачной плёнки с нарисованными на ней линиями. Она складывает его пополам, как показано на рисунке. Что она увидит?

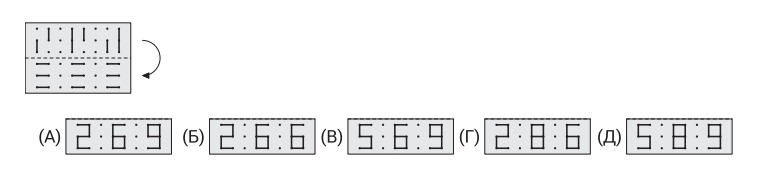
Ответ: В

11. Мастер хочет выложить плиткой пол, используя плитки только одной формы. Зазоры и пропуски не допускаются. Плитка какой формы не может быть использована?

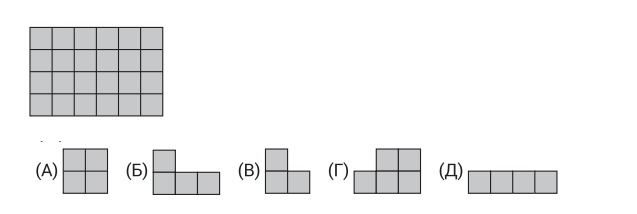
Ответ: Г

12. У Жени имеется 150 монет. Когда она бросила их на стол, 40% из них легли орлом вверх, и 60% — решкой вверх. Сколько монет, упавших решкой вверх, ей нужно перевернуть, чтобы количество монет, лежащих орлом вверх, и количество монет, лежащих решкой вверх, стало равным?

А) 10
Б) 15
В) 20
Г) 25
Д) 30

9-11 классы

1. По дороге в школу Маше пришлось бежать, чтобы успеть на автобус. Через две остановки она вышла и пошла дальше пешком. Какой из следующих графиков зависимости скорости от времени лучше всего представляет её дорогу до школы?

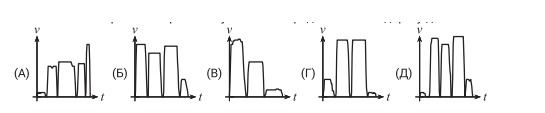
Ответ: Г

2. Целые положительные числа m и n являются нечётными. Какое из следующих целых чисел также является нечётным?
А) m(n+1)
Б) (m+1)(n+1)
В) m+n+2
Г) mn+2
Д) m+n

3. Внутри большого квадрата со стороной 10 см расположен меньший квадрат со стороной 4 см (смотри рисунок). Соответствующие стороны двух квадратов параллельны, и их центры совпадают. Какой процент площади большого квадрата закрашен серым цветом?

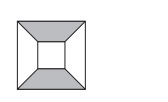
А) 35%
Б) 37%
В )40%
Г) 42%
Д) 45%

4.Сегодня четверг. Какой день недели будет через 2023 дня?
А) вторник
Б) среда
В) четверг
Г) пятница
Д) суббота

5.Прямоугольник ABCD составлен из 30 одинаковых квадратов. Периметр закрашенной фигуры равен 240 см. Чему равна площадь прямоугольника ABCD?

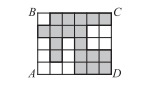
А) 1080 см2
Б) 1450 см2
В) 1580 см2
Г) 1920 см2
Д) 2430 см2

6. Семья состоит из пяти человек. Сумма их возрастов — 80 лет. Двум самым младшим членам этой семьи — 6 и 8 лет. Какова была сумма возрастов членов этой семьи 7 лет назад?

А) 35
В) 36
В) 45
Г) 46
Д) 66

7. Деревянный забор состоит из ряда вертикальных досок, каждая из которых соединена со следующей четырьмя горизонтальными досками. Первая и последняя доски в заборе вертикальные. Какое из следующих чисел может быть общим количеством досок в заборе?

А) 95
Б) 96
В) 97
Г) 98
Д) 99

8. В выражении a/5=7/b буквы a и b заменяют целыми положительными числами так, чтобы равенство было верным. Сколькими различными способами это может быть сделано?

А) 0
Б) 1
В) 2
Г) 3
Д) 4

9. После того как Вся выиграл 200 партий в шахматы, процент его побед составил 49%. Какое наименьшее количество дополнительных игр ему нужно выиграть, чтобы увеличить процент побед до 50%?

Ответ: Г

10. В каждой вершине треугольной пирамиде записано по целому положительному числу, а на каждом ребре указана сумма двух чисел, записанных в вершинах, которое это ребро соединяет. Какое число должно стоять на месте знака вопроса?

Ответ: Д

11. Женя решила экономить воду. Она сократила время, в течение которого умывается, на четверть. Она так же снизила напор воды, чтобы на четверть уменьшить скорость ее вытекания из крана. На какую долю Женя уменьшила общее количество воды, которое она использует для умывания?

А) 1/4
Б) 3/8
В) 5/8
Г) 5/12
Д) 7/16

12. На рисунке изображены три квадрата со сторонами 3 см, 5 см, 8 см. Какова площадь закрашенной фигуры?

А) 13 см^2
Б) 55/4^2
В) 61/4^2
Г) 65/^2
Д) 69/^2

13. Провод длиной 95 м разрезали на 3 части так, чтобы длина каждого следующего куска была на 50% больше, чем длина предыдущего. Какова длина самого большого куска провода?

А) 36 м
Б) 42 м.
В) 45 м.
Г) 46 м
Д) 48 м.

14. М и N – середины двух противоположных сторон прямоугольника. Какая часть прямоугольника закрашена?

А) 1/6
Б) 1/5
В) 1/4
Г) 1/3
Д) 1/2

15. У исследователя есть два сплава: первый сплав содержит 90% золота, а второй 54% золота. Он смешал 320 граммов первого и 160 граммов второго сплава, получив третий сплав. Сколько процентов золота содержится в получившимся сплаве?

А) 33%
Б) 48%
В) 65%
Г) 72%
Д) 78%

Источник: otvetuznay.ru

55 математических загадок, для решения которых нужна логика и воображение

Математические задачки на сообразительность (с ответами)

Думаете, математические загадки на счет и логику — это только для школьников? Как бы не так! Взрослым также полезно тряхнуть стариной и немного размять мозги при помощи не очень сложных, но интересных и не всегда стандартных загадок на счет.

Готовы проверить себя при помощи 55 вопросов? Если да, то пролистывайте ниже, начинаем решать задачки!

Вопросы всегда будут сопровождаться ответом, который вы увидите ниже. Но только не подглядывать!

1. Какое число получится, если перемножить все цифры на цифровой клавиатуре телефона?

Ответ:

Ноль, потому что любое число, умноженное на 0, всегда будет равно нулю.

2. Где можно прибавить 2 к 11 и получить 1?

Ответ:

3. Утка получила 9 долларов, паук — 36 долларов, пчела — 27 долларов. Основываясь на этой информации, сколько денег дадут кошке?

Ответ:

18 долларов (4,50 доллара за лапу).

4. Когда Джошу было 8 лет, его брат был вдвое моложе его. Теперь, когда Джошу 14 лет, сколько лет его брату?

Ответ:

Его брату 10 лет. Половина от 8 равна 4, поэтому брат Джоша на 4 года младше. Когда Джошу 14, его брат все еще на 4 года моложе, так что ему 10.

Raghav Modi / unsplash.com

5. Когда отцу был 31, мне 8. Сейчас он в два раза старше меня. Сколько мне лет?

Ответ:

Разница в возрасте 23 года, поэтому сыну должно быть 23 года, если отец был в два раза старше.

Смотрите также

6. Сколько сторон у круга?

Ответ:
Две — внутри и снаружи.

7. Что тяжелее — килограмм железа или килограмм пуха?

Ответ:

Вес их одинаковый.

8. Какая цифра чаще всего встречается между числами от 1 до 1000 включительно?

Подсказка: ищите закономерность!

Ответ:

Самая распространенная цифра — 1! Вы поняли, почему? Каждое число от 1 до 9 встречается ровно одинаковое количество раз в каждых десяти числах. Но поскольку было включено число 1000, цифра 1 появляется в числовом ряде на один раз больше.

Итак, всего цифра 1 встречается 301 раз, в то время как все остальные числа встречаются в ряде по 300 раз.

9. Сколько кирпичей нужно, чтобы построить здание из кирпича?

Ответ:

Только один — «последний».

10. Бита и мяч стоят 1 доллар 10 центов. Бита стоит на один доллар дороже, чем мяч. Сколько стоит мяч?

Ответ:

Если бы мяч действительно стоил 10 центов, то бита, которая дороже его на 1 доллар, стоила бы 1 доллар + 10 центов. Это противоречит условиям задачи. Давайте разберем решение. Допустим, цена мяча — X. Бита стоит на 1 доллар больше — Х + 1. Получаем такое уравнение: Х + (Х + 1) = 1,1, потому что вместе бита и мяч стоят 1,1 доллара. Решаем уравнение:

Значит, мяч стоит 5 центов, а бита — 1,05 доллара.

Смотрите также

11. Сможете ли вы расставить четыре девятки так, чтобы получилось 100?

Ответ:

12. Когда Джону было шесть лет, он забил гвоздь в свое любимое дерево, чтобы отметить свой рост. Десять лет спустя, в возрасте шестнадцати лет, Джон вернулся, чтобы посмотреть, насколько выше был гвоздь. Если бы дерево каждый год росло на пять сантиметров, насколько выше был бы гвоздь?

Ответ:

Гвоздь будет на той же высоте, так как деревья растут с верхушки.

13. Когда Митчу было 6 лет, его младшей сестре Лайле исполнилось полгода. Если Митчу сегодня 40 лет, то сколько лет Лайле?

Ответ:

Michal Matlon / unsplash.com

14. Вам даны 3 положительных числа. Вы можете сложить эти числа и умножить их вместе. Результат, который вы получите, будет одинаковым в обоих случаях. Какие числа?

Ответ:

1+2+3=6
1*2*3=6
И сложение, и умножение дают один и тот же результат.

15. Позавчера мне было 21, а в следующем году будет 24. Какого дня у меня день рождения?

Ответ:

Если нынешний день 1 января, то день рождения у тебя 31 декабря. Позавчера (30 декабря) тебе было еще 21 год, вчера (31 декабря) исполнилось 22 года, в нынешнем году исполнится 23 года, а в следующем году — 24 года.

16. Прибавь меня к себе и умножь на 4. Раздели меня на 8, и ты снова получишь меня. Какое я число?

Ответ:

17. Как футбольный фанат узнал перед игрой, что счет будет 0:0?

Ответ:

Перед игрой счет всегда 0:0.

18. Если умножить это число на любое другое число, ответ всегда будет один и тот же. Какое это число?

Ответ:

19. Какое следующее число в ряду? 7645, 5764, 4576, …

Ответ:

6 457, потому что последняя цифра перемещается вперед, чтобы получить следующее число в ряду.

20. Что можно поставить между 7 и 8 так, чтобы результат был больше семерки, но меньше восьмерки?

Ответ:

Это 7,8. Оно больше 7, но меньше 8.

21. Если два — компания, а три — толпа, то что такое четыре и пять?

Ответ:

22. Больше часа, меньше минуты

Ответ:

Aron Visuals / unsplash.com

23. Старая бабушка Адамс оставила половину своих денег внучке и половину этой суммы внуку. Она оставила шестую часть своему брату, а остаток, 1000 долларов, приюту для собак. Сколько всего она оставила?

Ответ:

Хитрость заключается в том, чтобы сосредоточиться не на гипотетических суммах, а на дробях: сложение половины, четверти и одной шестой говорит нам, что сумма составляет долю двенадцати (2+4+6=12). Вы также можете представить это как 6/12, 3/12, 2/12, что равняется 11/12. Если остаток составляет 1000 долларов, это должна быть одна двенадцатая, поэтому общая сумма составляет 12 000 долларов.

Смотрите также

24. Вы знаете, что 2 + 2 равно 2×2. Теперь найдите набор из трех различных целых чисел, сумма которых равна их сумме при умножении

Ответ:

Три различных целых числа, сумма которых при умножении равна их сумме, это 1, 2 и 3.

25. Какое число уменьшится на 12 единиц, если его записать и перевернуть лист вверх тормашками?

Ответ:

Ответ 86. Если лист с этим числом перевернуть, то получится 98, что на 12 больше, чем 86.

26. Если бы сейчас было на два часа позже, то до полуночи оставалось бы в два раза меньше времени, чем если бы сейчас было на час позже. Сколько сейчас времени?

Ответ:

27. Женщина идет по улице ночью в постоянном темпе. Когда она проходит мимо уличного фонаря, она замечает, что ее тень становится длиннее. Движется ли верхняя часть ее тени быстрее, медленнее или одинаково, когда тень длиннее, чем когда она короче?

Ответ:

Эта точка сохраняет постоянную скорость, не зависящую от длины тени.

28. У строителя 8 кирпичей. Семь из них весят одинаково, а один немного тяжелее. Как ему, используя весы, найти более тяжелый кирпич за два взвешивания?

Ответ:

Разделим кирпичи на 2 группы: первая группа — 6 кирпичей, вторая группа — 2 кирпича. На каждую чашу весов кладем по 3 кирпича из первой группы. Возможны два варианта после взвешивания:

Перевесит одна из чаш весов.
Весы сохранят равновесие.
В первом случае кладем на каждую чашу весов по одному кирпичу из более тяжелой группы. Если весы сохранят равновесие, то бракованный — третий кирпич из этой группы, если одна из чаш перевесит — бракованный кирпич находится на этой чаше.

Во втором случае кладем на каждую чашу весов по одному кирпичу из второй группы. Перевесит чаша, на которой находится бракованный кирпич.

29. Два мальчика играли в шашки 2 часа. Сколько времени играл каждый мальчик?

Ответ:

30. Мужчина умирает от старости в свой 25-й день рождения. Как это возможно?

Ответ:

Он родился 29 февраля.

JD Mason / unsplash.com

31. Если вы находитесь в 80 сантиметрах от двери и с каждым шагом продвигаетесь на половину расстояния до двери, сколько ходов потребуется, чтобы добраться до двери?

Ответ:

Вы никогда не дойдете до двери, потому что она всегда будет отстоять на половину расстояния, каким бы малым оно ни было.

32. Если на каждый цветок сядет по одной пчеле, то одна пчела останется без цветка, а если на каждый цветок сядет по 2 пчелы, то один цветок останется без пчелы. Сколько цветков и пчел?

Ответ:

4 пчелы и 3 цветка.

Смотрите также

33. Если вы идете в кино и берете с собой друзей, дешевле будет сводить одного друга в кино дважды или двух друзей в кино одновременно?

Ответ:

Дешевле взять двух друзей одновременно.

34. В каком месяце 28 дней?

Ответ:

35. Какое число увеличивается и не уменьшается?

Ответ:

36. У вас 4 яблока, вы убираете 3, сколько у вас останется?

Ответ:

37. Если вы покупаете петуха для несения яиц и рассчитываете получать по три яйца каждый день на завтрак, сколько яиц у вас будет через три недели?

Ответ:

Нисколько, потому что петухи не несут яиц.

榮達陳 / unsplash.com

38. Мельник пошел на мельницу и увидел в каждом углу по 3 кошки. Сколько ног на мельнице?

Ответ:

39. 6 человек построили сарай за 9 часов. За какое время построят этот же сарай 12 строителей?

Ответ:

Ни за сколько, потому что он уже построен.

Смотрите также

40. У фермера 17 овец, и все, кроме 9, умирают. Сколько осталось?

Ответ:

41. Поезд длиной 300 метров движется со скоростью 300 метров в минуту и должен пройти через тоннель длиной в 300 метров. За какое время поезд проедет тоннель?

Ответ:

Две минуты, потому что передней части поезда требуется одна минута, а остальной части поезда потребуется две минуты, чтобы пройти весь тоннель.

42. Я добавляю пять к девяти и получаю два. Ответ правильный, но как?

Ответ:

Когда будет 9 часов вечера, прибавьте к этому 5 часов, и вы получите 2 часа дня.

43. В странном маленьком городке был странный маленький ручеек со странными маленькими рыбками в странной маленькой стае. Незнакомец подошел к местному рыбаку и спросил, сколько весит его странная рыбка. Странный человечек ответил: «Вся рыба в этом ручье весит ровно ½ килограмм плюс ½ рыбы. Разве это не странно?» Сколько килограмм весит странная маленькая рыбка?

Ответ:

44. Вы положили на стол три спички, а затем попросили друга добавить еще две спички, чтобы получилось восемь. Как он сможет это сделать?

Ответ:

Из двух спичек составьте римскую цифру пять и прибавьте ее к трем, чтобы получилась римская цифра восемь.

45. У девочки столько же братьев, сколько и сестер, только у каждого брата вдвое меньше братьев, чем сестер. Сколько братьев и сестер насчитывает эта семья?

Ответ:

Четыре сестры и три брата.

46. Мужчина в два раза старше своей младшей сестры. Он также вдвое моложе их отца. Через 50 лет возраст сестры станет вдвое меньше возраста их папы. Сколько лет мужчине сейчас?

Ответ:

Смотрите также

47. Если семь человек встретятся друг с другом и каждый пожмет друг другу руку только один раз, сколько будет рукопожатий?

Ответ:

48. Три врача сказали, что Билл их брат. Но Билл утверждает, что у него нет братьев. Сколько же в реальности братьев у Билла?

Ответ:

Ни одного. У него три сестры — врачи по профессии.

49. Как вы можете сделать следующее уравнение верным, проведя только одну прямую линию: 5+5+5 =550. Ты можешь в этом разобраться?

Ответ:

Есть два способа сделать это:

Нарисуйте линию на первом знаке плюс, чтобы превратить его в 4.
Замените символ равенства на перечеркнутый символ равенства, что означает «не равно».

50. В парке 8 скамеек. Три покрасили.
Сколько скамеек стало в парке?

Ответ:

51. Яблоко — 60 копеек, банан — 60 копеек, грейпфрут — 60 копеек. Сколько стоит груша?

Ответ:

120 копеек, потому что цена каждого фрукта рассчитывается путем умножения количества гласных на 20.

52. Анна написала все числа от 300 до 400 на листе бумаги. Сколько раз она написала цифру 3?

Ответ:

53. Сколько раз на протяжении суток минутная и часовая стрелки часов образуют прямой угол?

Ответ:

За 1 час часовая стрелка описывает угол 30°, а за 1 мин. − угол 0,5°. Минутная стрелка за 1 мин. описывает угол 6°. Так как 90 : (6 − 0,5) = 16 (4 / 11), минутная и часовая стрелки образуют прямой угол в первый раз через 16 (4 / 11) мин. после того, как обе будут стоять на 12. Так как n × 16 (4/11) = 24 × 60, мы получаем n = 88 (в это число входят углы в 0°, 90°, 180° і 270°, образованные минутной и часовой стрелками).

Смотрите также

54. Расставьте скобки и математические знаки так, чтобы равенство было верным: 9999999 = 100

Ответ:

(99-99)* 999 = 10*0 и еще рядом других способов.

Drew Beamer / unsplash.com

55. Что всегда будет находиться перед вами и при этом вам его никогда не увидеть?

Ответ:

Источник: 1gai.ru