Научный руководитель: Ф.И.О. Тютина Надежда Валентиновна, учитель математики
Содержание работы:
Введение
Гипотеза исследования
Ход исследования
Ход 1
Ход 2
Ход 3
Применение
Моё выступление и опрос
Мой правильный паркет с рисунком
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Математик, также как и художник или поэт, создает узоры.(Г. Харди.)
Правильные паркеты. Мозаика
Правильные паркеты – это бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Покрытие плоскости может составляться из одинаковых правильных многоугольников, из разных правильных многоугольников, из не правильных многоугольников, из произвольных фигур, при котором многоугольники имеют общую сторону, либо общую вершину или совсем не имеют общих точек. Чаще говорят просто – геометрическая мозаика.
Мозаика выглядит очень красиво, если она построена согласно определению. В работе я рассмотрю мозаики в которых используются правильные геометрические фигуры на плоскости. Но, тем не менее покажу примеры хаотичной мозаики, которая выкладывается в определённый рисунок.
Построение правильного восьмиугольника.
Рассмотрим какими же правильными многоугольниками можно замостить плоскость вокруг одной точки без просвета?
Правильный паркет можно составить из равносторонних треугольников, квадратов и из правильных многоугольников.
Посмотрим сколько может сходиться правильных многоугольников в одной вершине. Для этого 360_7=51,43……0; 360_6=60. Таким образом получаем, что при схождении в одной вершине семи и более многоугольников хотя бы один угол в правильном многоугольнике получается должен быть менее 60, а это невозможно, поскольку у правильного треугольника он 60, а меньше нет многоугольника нет. Также не может быть, чтобы при схождении в одной вершине двух многоугольников у одного из них внутренний угол был бы более 180.
В итоге, возможны лишь варианты, когда в вершине сходятся 3, 4, 5 и 6 правильных многоугольников.
Цели исследования:
— Закрепить знания о свойствах правильных многоугольников в процессе исследования вопроса о покрытии плоскости правильными многоугольниками.
— Обосновать с помощью математических фактов, как можно уложить правильный паркет на плоскости вокруг одной точки без просвета.
— Убедиться в практической значимости исследуемой темы.
— Придумать узор своему паркету на основе выбранного правильного многоугольника.
Задачи, стоящие передо мной
— Выяснить как устроен правильный паркет (геометрическая мозаика) на плоскости?
— Определить из скольких разных фигур правильных многоугольников
можно сложить правильный паркет на плоскости вокруг одной точки без просвета?
— Выяснить значимость изучаемой работы в нашей жизни.
ГИПОТЕЗА ИССЛЕДОВАНИЯ
Вокруг одной точки можно уложить плоскость правильными многоугольниками без просвета:
С помощью правильных многоугольников:
Восьмиконечная звезда или правильный звёздчатый восьмиугольник
Шестью правильными треугольниками;
Четырьмя правильными четырехугольниками (квадратами);
Тремя правильными шестиугольниками.
С помощью правильных многоугольников двух различных форм:
Тремя треугольниками и двумя четырёхугольниками;
Четырьмя треугольниками и одним шестиугольником;
Двумя треугольниками и двумя шестиугольниками;
Одним четырёхугольником и двумя восьмиугольниками;
Одним треугольником и двумя двенадцатиугольниками.
С помощью правильных многоугольников трех различных форм:
Одним треугольником, двумя четырёхугольникамии одним шестиугольником;
Двумя треугольниками, одним четырёхугольником и одним двенадцатиугольником;
Одним четырёхугольником, одним шестиугольником и одним двенадцатиугольником.
ХОД ИССЛЕДОВАНИЯ
Ход I
Обозначим через n число сторон правильного многоугольника, тогда 180(n–2) – сумма всех внутренних углов многоугольника.
Сумма углов, сходящихся в одной точке равна 360 (полный круг).
Для правильных многоугольников наименьшее число n равно 3.
1) Если n = 3, то плоскость возможно уложить правильными треугольниками, их число равно 360 : 60 = 6.
2) Если n = 4, то плоскость возможно уложить правильными четырехугольниками,их число равно 360 : 90 = 4.
3) Если n = 6, то плоскость возможно уложить правильными шестиугольниками, их число равно 360 : 120 = 3.
Если n = 5 и n > 6 значение дроби больше 120 и правильных многоугольников не существует.
Вывод первый:
Вокруг одной точки можно уложить плоскость без просвета, следующими одноимёнными правильными многоугольниками:
— шестью правильными треугольниками;
— четырьмя квадратами;
— тремя правильными шестиугольникам.
Ход II
1) Обозначим n – количество треугольников, m – количество квадратов, тогда согласно гипотезе должно выполняться равенство 60n+90m=360.
Рассмотрим следующие случаи:
а) Если n = 1, то 90m = 360- 60·1; 90m = 300; m не целое .
При n = 1, задача решений не имеет.
б) Если n = 2, то 90m = 360- 60·2; 90m = 240; m не целое.
При n = 2, задача решений не имеет.
в) Если n = 3, то 90m = 360 — 60·3; 90m = 180; m = 2.
При n = 3, m = 2 задача имеет решение.
г) Если n = 4, то 90m = 360- 60·4; 90m = 12; m не целое .
При n = 4, задача решений не имеет.
д) Если n = 5, то 90m = 360- 60·5; 90m = 60; m не целое .
При n = 5, задача решений не имеет.
Примечание: при n больше пяти, задача решений не имеет, так как сумма получается больше 360.
2) Обозначим n – количество треугольников, m – количество шестиугольников, тогда согласно гипотезе должно выполняться равенство 60n+120m=360.
Рассмотрим следующие случаи:
а) Если n = 1, то 120m = 360- 60·1; 120m = 300; m не целое .
При n = 1, задача решений не имеет.
б) Если n = 2, то 120m = 360- 60·2; 120m = 240; m =2.
При n = 2, m = 2 задача имеет решение.
в) Если n = 3, то 120m = 360- 60·3; 120m = 180; m не целое.
При n = 3, задача решений не имеет.
г) Если n = 4, то 120m = 360- 60·4; 120m = 120; m =1.
При n = 4, m = 1 задача имеет решение.
д) Если n = 5, то 120m = 360- 60·5; 120m = 60; m не целое
При n = 5, задача решений не имеет.
Примечание: при n, больше пяти, задача решений не имеет, так как сумма получается больше 360.
3)Обозначим n – количество квадратов, m – количество восьмиугольников, тогда согласно гипотезе должно выполняться равенство 90n+135m=360.
Рассмотрим следующие случаи:
а) Если n = 1, то 135m = 360- 90·1; 135m =270; m =2.
При n = 1, m = 2 задача имеет решение.
б) Если n = 2, то 135m = 360- 90·2; 135m = 180; m не целое.
При n = 2, задача решений не имеет.
в) Если n = 3, то 135m = 36- 9·3; 135m = 9; m не целое.
При n = 3, задача решений не имеет.
г) Если n = 4, то 135m = 360-90·4; 135m =0; m не целое.
При n = 4, задача решений не имеет.
Примечание: при n, больше четырёх, задача решений не имеет, так как сумма получается больше 360.
4) Обозначим n – количество треугольников, m – количество двенадцатиугольников, тогда согласно гипотезе должно выполняться равенство 60n+150m=360.
Рассмотрим следующие случаи:
а) Если n = 1, то 150m = 360- 60·1; 150m =300; m =2
При n = 1, m = 2 задача имеет решение
б) Если n = 2, то 150m = 360 — 60·2; 150m = 240; m не целое.
При n = 2, задача решений не имеет.
в) Если n = 3, то 1500m = 3600- 600·3; 1500m = 1800; m =18/15.
При n = 3, задача решений не имеет.
Примечание: при n, больше трех, задача решений не имеет, так как сумма получается больше 360.
Вывод второй:
Вокруг одной точки можно уложить плоскость без просвета, следующими правильными многоугольниками двух различных форм:
— тремя треугольниками и двумя четырёхугольниками
— четырьмя треугольниками и одним шестиугольником
— двумя треугольниками и двумя шестиугольниками
— одним четырёхугольником и двумя восьмиугольниками
— одним треугольником и двумя двенадцатииугольниками.
Ход III
1) Обозначим n – количество треугольников, m – количество четырёхугольников, k — количество шестиугольников,
тогда согласно гипотезе должно выполняться равенство
60n+90m+120k =360.
Рассмотрим следующие случаи:
а) Если n=1, m=1, то 120k=360-60·1-90·1; 120k=210; k не целое .
При n = 1, m =1, задача решений не имеет.
б) Если n = 1, m =2, то 120k = 360- 60·1- 90·2; 120k = 120; k =1.
При n = 1, m = 2, k =1, задача имеет решение
в) Если n = 2, m =1, то 120k = 360- 60·2- 90·1; 120k = 1500; k не целое .
При n = 2, m =1, задача решений не имеет.
Примечание: при n, больше трех, задача решений не имеет, так как сумма получается больше 360.
2) Обозначим n – количество треугольников, m – количество квадратов,
k — количество двенадцатиугольников, тогда согласно гипотезе должно выполняться равенство
60n+90m+150k =360.
Рассмотрим следующие случаи:
а) Если n = 1, m =1, то 150k = 360 — 60·1-90·1; 150k = 210; k не целое .
При n = 1, m =1, задача решений не имеет.
б) Если n = 2, m =1, то 150 = 360- 60·2-90·1; 150k = 150; k =1.
При n = 2, m = 1, k =1, задача имеет решение
Примечание: при n, больше трех, задача решений не имеет, так как сумма получается больше 360.
3) Обозначим n – количество четырёхугольников, m – количество шестиугольников, k — количество двенадцатиугольников,
тогда согласно гипотезе должно выполняться равенство
90n+120m+150 k =360.
Рассмотрим следующие случаи:
а) Если n = 1, m =1, то 150k = 360- 90·1- 120·1; 150k = 150; k =1.
При n = 1, m =1, k =1, задача имеет решение
Примечание: при n, больше двух, задача решений не имеет, так как сумма получается больше 360.
Вывод третий:
Вокруг одной точки можно уложить плоскость без просвета, следующими правильными многоугольниками трех различных форм:
— одним треугольником, двумя четырёхугольниками и одним шестиугольником.
— двумя треугольниками, одним четырёхугольником и одним двенадцатиугольником.
— одним четырёхугольником, одним шестиугольником и одним двенадцатиугольником.
ПРИМЕНЕНИЕ
Проведённая работа показывает как теоретическое, так и практическое применение геометрического материала, а так же помогает увидеть достаточно обширное применение рассмотренного материала в жизни.
Правильные паркеты (геометрическая мозаика) широко встречается и используется
В строительстве и ремонте жилых помещений:
полы в жилых помещениях застилают паркетами,
стены ванных комнат покрывают кафельными плитками,
современные здания украшают мозаиками.
В спортивных играх: например
шахматная доска, сетка в играх с мячом и шайбой, пошив мяча.
В декоративно — прикладном искусстве:
вышивка на коврах, гобеленах, решетки на окнах
В пчеловодстве — пчелиные соты (вощина)
МОЁ ВЫСТУПЛЕНИЕ И ОПРОС
С данным материалом я выступил перед своими одноклассниками. Показал презентацию, рассказал и провёл опрос о полезности и значимости материала.
Вопросы были следующие:
Вам знакомо понятие «Мозаика»?
Знали ли Вы что такое «Правильный паркет (геометрическая мозаика)»?
Удалось ли мне Вас заинтересовать?
Как думаете часто ли в математике при доказательствах и исследованиях применяются похожие на мои рассуждения?
Смогли бы теперь сами повторить рассуждения и построить правильный паркет?
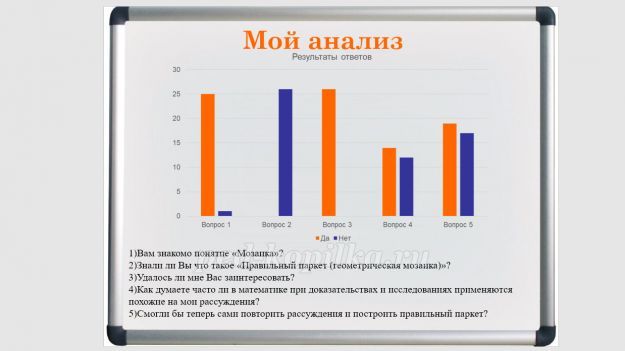
Я переработал полученные ответы, и построил диаграмму. Принимало участие 26 человек.
1) Да-25 Нет-1
2) Да-0 Нет-26
3) Да-26 Нет-0
4) Да-14 Нет-12
5) Да-19 Нет-7
МОЙ ПРАВИЛЬНЫЙ ПАРКЕТ С РИСУНКОМ
На основе паркета из квадратов я построил свой паркет, самостоятельно придумав рисунок.
Этапы выполнения работы представлены на рисунках.

ЗАКЛЮЧЕНИЕ
В вершине правильного паркета (геометрической мозаики) может сходиться не более шести и не менее трех многоугольников.
Существует только конечное число правильных паркетов: 11.
Я научился видеть различные правильные паркеты в жизни, выступил на уроке математики и провёл опрос о том насколько полезной была информация.
Построил свой рисунок на правильном паркете с основой — квадрат.
« Геометрия как один из разделов математики — это не только стройная система законов, но и уникальное средство познания мира».
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Геометрия 7 – 9 , учебник для общеобразовательных школ. П.С. Атанасян, В.Ф.Бутузов и другие,13 – е издание, Просвещение , 2003 г.
2. Иванов И.И. «Метод проектов», Учебное пособие, 1999 г.
3. Щепан Еленьский «Занимательная математика, 1961 г.
4. Журнал «Математика в школе» , № 3 (1993 г.).
5. Г.Штейнгауз «Математический калейдоскоп, библиотечка «Квант», №8,1981г.
6. Журналы 1-е сентября 1992г., 1994г.
7. Интернет ресурсы
Источник: ped-kopilka.ru
решебники и ГДЗ
Если Вы не нашли свой учебник — пишите нам на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. и мы обязательно добавим его на наш сайт.
Будем благодарны за предложения и пожелания от Вас по улучшению работы сайта.
На нашем сайте Вы найдете решебники (гдз – готовые домашние задания) по всем предметам школьной программы – математике, русскому языку, истории, литературе, географии, английскому языку и т.д.
В настоящее время представлены решебники по математике Виленкина, Зубаревой, Дорофеева, Бунимовича, Жохова, Чеснокова, Шварцбурда, Мордковича, Петерсона, Кузнецовой, Минаевой.
В ближайшее время мы добавим решебники и гдз по русскому языку.
О том, какие готовые домашние задания нужны в первую очередь – решать только Вам. Напишите нам, и мы в кратчайшие сроки добавим необходимый Вам решебник на наш сайт.
О том, нужны ли решебники споры не утихают ни на миг. У каждой стороны – и противников и сторонников решебников — есть веские аргументы в защиту своего мнения.
Из плюсов можно выделить следующие моменты:
А. Есть возможность проверить правильность своего решения задачи.
Б. Если упражнение не получается решить, непонятно условие задачи или что-то еще подобное – можно посмотреть решебник. Как правило, все задания решены с объяснениями.
В. Решебники (гдз) просто необходимы родителям чтобы помочь своему ребенку в выполнении домашнего задания. Ведь как бы хорошо Вы не учились в школе, со временем какие-то моменты все равно забываются. И с помощью гдз Вы можете восполнить пробелы в своих знаниях, чтобы в доступной форме объяснить своему ребенку непонятный для него материал.
Из существенных минусов можно выделить только один – школьник вместо того, чтобы самому решать задания станет просто списывать из интернета готовые решения задач.
В реальности – все зависит не только от самого школьника, но и в большей степени от родителей, во вред или во благо будут использованы решебники с готовыми домашними заданиями – ГДЗ.
Источник: klass-6.ru
Презентация на тему Паркеты
Паркетом называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.
Слайд 1Паркеты
Выполнил:
Ученик 8 А класса
Подзоров Денис
«С помощью математики мы только откроем дверь,
ведущую в другой мир, и будем любоваться садом, лежащим за ней» — говорил Мориц Корнелиус Эшер, создавая геометрические объекты, которые пользуются спросом и считаются «писком» моды до сих пор!

Слайд 2Паркетом называется такое заполнение плоскости многоугольниками, при котором любые два многоугольника
либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Слайд 3Какими же многоугольниками можно замостить плоскость?
Паркеты из одинаковых правильных многоугольников.
Сумма всех
углов n-угольника равна 180°(n-2).
Все углы правильного многоугольника равны; следовательно,
каждый из них равен 180°(n-2)/n.
В каждой вершине паркета сходится целое число углов;
поэтому число 2·180° должно быть целым кратным
числа 180°(n-2)/n.
Преобразуем отношение этих чисел: Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6.
Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.

Слайд 4Паркет называется правильным, если он состоит из правильных многоугольников и вокруг
каждой вершины правильные многоугольники расположены одним и тем же способом.

Слайд 5
Самый простой, но и самый скучный паркет получается, если плоскость разбить
на равные квадраты.
Здесь два квадрата имеют либо общую сторону,
либо общую вершину или совсем не имеют общих точек.
Столь же просты паркеты из правильных шестиугольников.
Паркеты из правильных многоугольников

Слайд 6Вероятно, вам случалось видеть паркет, составленный из правильных восьмиугольников и квадратов.
Красивый паркет можно составить из правильных шестиугольников, квадратов и равносторонних треугольников.

Слайд 7Паркет производит приятное впечатление, если он достаточно симметричен. Фигура называется симметричной,
если ее наложить на саму себя не «тривиальным» способом (т.е. не таким, когда все точки останутся на своем месте).

Слайд 8легко покрыть плоскость параллелограммами:
Вообще можно замостить плоскость копиями
произвольного
четырехугольника, необязательно выпуклого:
Паркеты из неправильных многоугольников
Источник: thepresentation.ru