Как сделать паркет из правильных многоугольников

Задание: Перечислите все правильные паркеты на поверхности сферы. Затем попытайтесь перечислить или хотя бы построить примеры паркетов на поверхности сферы. То же самое сделать для случая плоского тора. Под плоским тором геометры понимают обычный прямоугольник, у которого мысленно «склеены» противоположные стороны.

Для начала определим, что же такое паркет.

Паркет (мозаика) — бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек.

Итак, плоскость можно без зазоров покрыть треугольниками, параллелограммами и центрально-симметричными шестиугольниками.

Для того, чтобы убедить в том, что никакой другой правильный многоугольник паркета не образует, нам понадобится всего лишь формула суммы углов многоугольника.

Если паркет составлен из n-угольников, то в каждой верши­не данного паркета будет сходиться m = 360°/ k n многоугольников, где k n — угол правильного n-угольника. 360° делится нацело на k n только при n =3, n=4 и n =6 (если брать n≤7), соответственно другие правильные многоугольники паркета не образуют.

Геометрия 9 класс (Урок№26 — Построение правильных многоугольников.)

Например, у правильного пятиугольника угол при вершине равен 108°. Если сложить три пятиугольника, то останется зазор в 36°, а если четыре, то они станут накладываться друг на друга (сумма углов при вершинах будет равна 432°, что превышает 360°). Для многоугольников с числом сторон большим шести наложение возникает уже при попытке сложить вместе три фигуры (поскольку углы правильного n-угольника равны 180°-360°/n). Попытка покрыть плоскость правильными пятиугольниками представлена ниже.

Если же взять правильный пятиугольник на сфере, то при определенных размерах его углы станут равными 120 градусам (а не 108, как на плоскости) и три таких пятиугольника будут без зазоров стыковаться друг с другом, если их сложить вершинами. Более того, 12 пятиугольников такого размера без зазоров покрывают всю сферу. По-другому, показанную фигуру можно представить, как проекцию ребер и граней правильного додекаэдра на описанную вокруг него сферу.

Правильный паркет – паркет из правильных многоугольников, в котором вокруг любой вершины многоугольники расположены одним и тем же способом (вокруг всех вершин в одном и том же порядке следуют многоугольники одних и тех же наименований).

На плоскости существуют только три правильных паркета: из правильных треугольников, из квадратов и из правильных шестиугольников. Правильность паркета означает сочетание трёх свойств:

1. У изогонального (вершинно-транзитивного) паркета «равноправны» все вершины, т.е. для любых двух вершин существует симметрия паркета, совмещающая первую вершину со второй.
2. У изотоксального (рёберно-транзитивного) паркета «равноправны» все рёбра, т.е. для любых двух рёбер существует симметрия паркета, совмещающая первое ребро со вторым.
3. У изоэдрического (гране-транзитивного) паркета «равноправны» все грани, т.е. для любых двух граней существует симметрия паркета, совмещающая первую грань со второй.

Под симметрией паркета здесь понимается такое перемещение плоскости, при котором весь паркет точно совмещается сам с собой. Легко убедиться, что сочетание всех трёх свойств возможно только для паркета, состоящего из одинаковых правильных многоугольников.

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnline

Итак, существует 11 правильных паркетов: 3 – из правильных k-угольников и еще 8 из комбинаций правильных многоугольников:

Правильные паркеты

В первом ряду представлены паркеты из однотипных правильных многоугольников, в остальных — из их комбинаций.

Примером паркета на поверхности сферы может являться обычный футбольный мяч. Паркет состоит из 12 пятигранников и 20 шестигранников.

В развёрнутом виде паркет может быть представлен следующим образом:

В то же время сфера может быть покрыта паркетом, состоящим из 12 сферических пятиугольников. Как уже было сказано, если взять правильный пятиугольник на сфере, то при определенных размерах его углы станут равными 120 o (а не 108 o , как на плоскости) и три таких пятиугольника будут без зазоров стыковаться друг с другом, если их сложить вершинами.

Это можно увидеть по чёрно-белым толстым линиям — узору на мяче.

Разбивая фигуры, из которых состоих паркет, на более мелкие «типичные» фигуры (например треугольники и квадраты), можно получить совершенно другой паркет. Кроме того новый паркет можно получить при объединении «типичных» фигур.

На тор, как я понимаю, можно накладывать более-менее те же паркеты, что и на сферу. На него, например, можно наложить простейший паркет из правильных четырёхугольников (квадратов) (с 3d я сама не дружу, поэтому картинку нашла только такую):

Источник: 4070pochinova.livejournal.com

Исследовательская работа «Правильные Паркеты»

В начале прошлого столетия великий» французский архитектор Корбюзье как-то воскликнул: «Все вокруг геометрия! ». Сегодня уже в начале 21 столетия мы можем повторить это восклицание с еще большим изумлением. В самом деле, посмотрите вокруг – всюду геометрия!

Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики. Все это создано руками человека, вооруженного геометрическими знаниями. На уроках геометрии мы изучали тему «Многоугольники», и я решила выяснить, где можно найти применение этой темы.

Если посмотреть вокруг, то можно увидеть, что в настоящее время для оформления интерьера квартир широко используют паркет. Паркеты имеют разную форму и окраску. Мне стало интересно, как создаются паркеты и как это связано с геометрией. На уроках геометрии изучается тема: «Многоугольники».

Приглядевшись внимательнее, я стала замечать эти многоугольники вокруг себя: паркет, линолеум, кафельная плитка, геометрические орнаменты в художественных изделиях, в оформлениях книг. А сколько же их может быть этих паркетов, встал передо мной вопрос? Как их так мудро и красиво соединяют? Этот материал мы еще не изучали, и передо мной встала

цель: подробно изучить паркеты.

Выдвинута проблема: определить количество правильных паркетов.

1. Изучить литературу, интернет-ресурсы по заданной теме.

1. Закрепить знания свойств правильных многоугольников в процессе исследования вопроса о покрытии плоскости правильными многоугольниками.
2. Обосновать с помощью математических фактов, как можно уложить паркет.
3. Оформить презентацию для защиты работы.

Выдвигаю гипотезу: количество правильных паркетов бесчисленное множество.

Объект исследования — паркеты.

Методы исследования: анализ научной, учебной литературы; сравнение и анализ результатов, полученных разными авторами; их систематизация; метод аналогии.

Во все времена и у всех народов в строительстве интерьера полам и их убранству уделялось большое внимание. Еще в древние времена в Египте, Индии, Китае, и во многих других странах создавали прочные и красивые полы. В средние века «паркету» стали уделять больше внимания, он стал неотъемлемой частью новых домов, дворцов и замков. Но своего художественного совершенства пол из «дубовых кирпичей» достигает к началу XVII века в разных странах Европы. Следует отметить, что художественная форма паркета тесно связана с общим стилистическим развитием искусства и архитектуры.

В общественных зданиях Древней Руси полы делали из дерева, досок или из «деревянных кирпичей». Начиная с XVI в. полы в России стали настилать из дубовых клепок, укладываемых рисунком, который носил название «елочка», а сам пол называли «косящатым». Клепки, как правило, укладывали на грубораспиленное основание из мягкой древесины, большей частью сосны. Исконное и широко распространенное народное искусство резьбы по дереву, а также навыки в художественной обработке и укладке пола в древнерусском зодчестве создали все предпосылки для быстрого развития художественного паркета в России.

Так, уже в XVII в. наиболее распространенным приемом укладки паркета был способ, называемый «дубовым кирпичом»: паркетины в форме кирпичей укладывали на известковой основе, швы между дубовыми кирпичами заливали известью, смешанной со смолой. Вдоль стен иногда делали дубовый бордюр.

Такой паркет знали на Руси и раньше, он уже был известен по Дмитровскому собору во Владимире, по храму Василия Блаженного и Донскому монастырю в Москве. Но в отличие от тех полов к концу XVII в. он стал более искусным в художественном отношении. Паркет начала XVIII в. связан с русской резьбой.

Высокохудожественная резьба по дереву и металлу процветала в XVII в. в московских мастерских Оружейной палаты. В 1711 г. Петр I закрыл эти мастерские, а всех резчиков перевел в Петербург на корабельные верфи. Эти кадры мастеров и были использованы адмиралтейством при изготовлении паркетов петербургских дворцов.

Паркет — лицевой слой пола, настилаемый по определенному рисунку из отдельных строганых дощечек (клепок). Паркетом называют также и сам материал, из которого выкладывается паркетный пол. Полы из паркета настилаются в жилых и общественных зданиях, они отличаются красивым внешним видом, малой тепло- и звукопроводностью.

Паркет из правильных многоугольников

Итак, чтобы определить кол-во правильных паркетов, прежде всего вспомним определение правильных многоугольников из учебника А. Атанасяна «Геометрия 7-9»:

«Правильным многоугольником называется выпуклый многогранник, у которого все углы и все стороны равны».

Что же называется правильным паркетом?

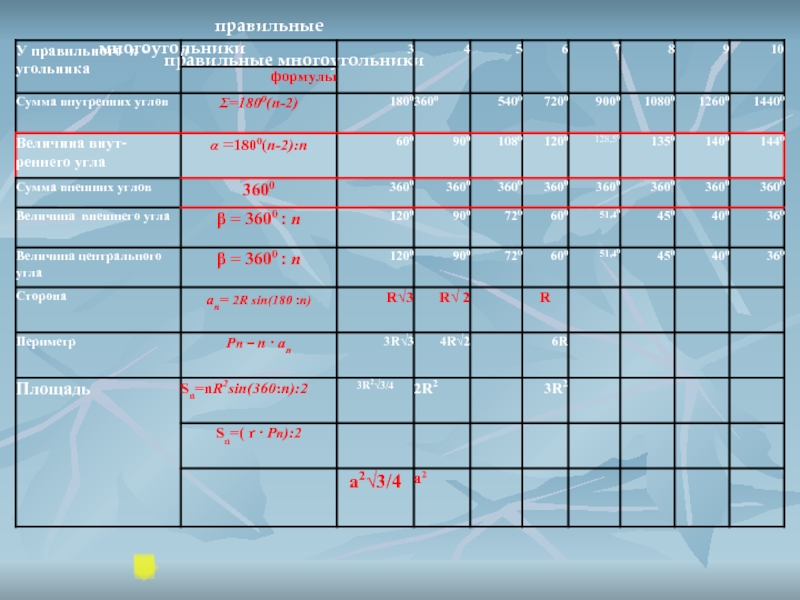
Обозначим через n число сторон правильного многоугольника, тогда n-2∙180° – сумма всех внутренних углов многоугольника. αn=n-2n∙180°- каждый угол правильного многоугольника.

Чтобы можно было сгруппировать вокруг какой – то точки определенное число одинаковых правильных многоугольников, необходимо, чтобы сумма их углов, сходящихся в данной точке, равнялось 360 .

Определение паркета: Паркетом называется заполнение плоскости многоугольниками, при котором любые два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо не имеют общих точек.

Паркет называется правильным, если он состоит из правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом.

Изучив литературу, я узнала, что паркетов, необязательно правильных существует бесчисленное множество. Однако, подобно тому как при бесчисленном множестве многогранников вообще существует лишь конечное число правильных многогранников, так и при бесчисленном множестве паркетов, существует лишь конечное число правильных паркетов.

I. Замощение окрестности точки плоскости правильными многоугольниками одного типа .

1. Паркеты, состоящие только из правильных треугольников.

Количество сторон: n=3 ;

Угол многоугольника: αn=n-2n∙180°=3-23∙180°=60°

Количество многоугольников: 360°:60°=6 – натуральное число.

1. Паркеты, состоящие из правильных четырехугольников (квадрат).

Количество сторон: n=4 ;

Угол многоугольника: αn=n-2n∙180°=4-24∙180°=90°

Количество многоугольников: 360°:90°=4 – натуральное число.

1. Паркеты, состоящие из правильных пятиугольников.

Количество сторон: n=5 ;

Угол многоугольника: αn=n-2n∙180°=5-25∙180°=108°

Количество многоугольников: 360°:108°=3,(3) – ненатуральное число.

1. Паркет, состоящие из правильных шестиугольников.

Количество сторон: n=6 ;

Угол многоугольника: αn=n-2n∙180°=6-26∙180°=120°

Количество многоугольников: 360°:120°=3

Итак , величина угла правильного n-угольника определяется по формуле αn=n-2n∙180°

Используя эту формулу , для различных значений получаем следующие величины углов правильных n-угольников

Источник: nsportal.ru

Презентация на тему Паркеты. Правильные, полуправильные

Слайд 1паркеты.
правильные,
полуправильные.

Слайд 2
Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.
паркет

Слайд 3Из
каких
правильных
многоугольников
можно
составить
паркет?

Слайд 4

Слайд 5
попытка №2 ,
из пятиугольников

увы. ничего не вышло.

Слайд 6

Слайд 7Необходимое усло-вие для построения паркета.

в
узле
360
градусов
Необходимое усло-вие для построения паркета.

Слайд 8

правильные многоугольники

Слайд 9теорема №1
Возле любого правильного многоугольника можно описать окружность .
теорема№2
В окружность

можно вписать правильный многоугольник.

Слайд 101. при n=3, то m=3600/600=6 треугольников в узле

n=3, то m=3600/600=6 треугольников в узле
2.при n=4 ,то m=3600/900=4

четырёхугольника в узле

3.при.n=5, то т=3600:1080=3.333333

При п>7 внутренние углы правильных п-угольников больше 1200. Кроме того внутренние углы правильного многоугольника всегда меньше1800 .
1200 3600/α > 3600/1800 ,
2 7 не существует правильных многоугольников для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников построить нельзя!

4 . при n=6 , то m=360:120=3 шестиугольника в узле

Слайд 11

Из правильных пятиугольников нельзя сложить паркет.
например:

Слайд 12вывод:
Только из этих правильных многоугольников можно построить правильный паркет.

Слайд 13

Слайд 14

Слайд 15Необходимое условие для построения паркета.

Необходимое условие для построения паркета.

Источник: theslide.ru