Треугольный паркет (треугольный паркетаж) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
Треугольная мозаика является двойственной шестиугольной мозаике — если соединить центры смежных треугольников, то проведённые отрезки дадут шестиугольную мозаику. Символ Шлефли треугольного паркета — , что означает, что в каждой вершине паркета сходятся 6 треугольников.
Внутренний угол правильного треугольника равен 60 градусов, так что шесть треугольника в одной вершине дают вместе 360 градусов. Это одна из трёх правильных мозаик плоскости. Другие две мозаики — шестиугольный паркет и квадратный паркет.
Английский математик Конвей называл мозаику deltille (дельта-мозаикой), поскольку она имеет форму греческой буквы дельта (Δ). Треугольную мозаику можно также назвать кис-шестиугольной мозаикой, если применить операцию kis, которая добавляет центральную вершину и треугольники, разбивая грани шестиугольной мозаики.
Геометрия — Построение правильного треугольника
Однородные раскраски
Существует 9 различных однородных раскрасок треугольной мозаики (по цветам 6 треугольников вокруг вершины — 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314). Три из них можно получить их других путём замены цветов — 111212 и 111112 из 121213, комбинируя 1 и 3, в то время как 111213 получается из 121314.
Существует один класс архимедовой раскраски, 111112, (помечен *), в котором раскраска не является 1-однородной и содержит перемежающиеся ряды треугольников, в которых каждый третий выкрашен. Приведённая раскраска является 2-однородной и таких имеется бесконечно много, поскольку такие раскраски определяются произвольными сдвигами строк.
Решётка A2 и упаковка кругов
Расположение вершин треугольной мозаики называется решёткой A2. Она является 2-мерным вариантом симлектических сот.
Решётка A*
2 (которая также называется A3
2) может быть построена как объединение трёх решёток A2 и эквивалентна решётке A2.
Вершины треугольной мозаики являются центрами наиболее плотной упаковки кругов . Любой круг соприкасается с 6 другими кругами (контактное число). Плотность упаковки равна π 12 >>> , это около 90,69 %. Поскольку объединение трёх решёток A2 снова будет решёткой A2, круги можно раскрасить в три цвета.
Ячейкой диаграммы Вороного треугольной мозаики является шестиугольник, так что мозаика Вороного, шестиугольная мозаика, имеет прямое отношение к упаковке кругов.
Геометрические варианты
Треугольные мозаики могут быть идентичны топологии правильной мозаики (6 треугольника в каждой вершине). Существует 5 вершинно транзитивных вариантов с одинаковыми гранями (транзитивных по граням). С точки зрения симметрии все грани имеют одинаковый цвет, раскраска же на рисунках представляет положение в сетке.
- Разносторонний треугольник
симметрия p2 - Разносторонний треугольник
симметрия pmg - Равнобедренный треугольник
симметрия cmm - Прямоугольный треугольник
симметрия cmm - Правильный треугольник
симметрия p6m
43 Четыре паркета, или Отражения треугольника относительно его сторон
Связанные многогранники и мозаики
Плоские мозаики связаны с многогранниками. Располагая меньше треугольников в каждой вершине, получим незаполненное пространство, что позволяет согнуть в фигуру в пирамиду. Отсюда можно получить правильные многогранники: пять, четыре и три треугольника в вершине дают икосаэдр, октаэдр и тетраэдр соответственно.
Эта мозаика топологически связана (как часть последовательности) с правильными многогранниками с символами Шлефли .
Эта мозаика топологически связана (как часть последовательности) с полуправильными многогранниками с конфигурацией граней Vn.6.6.
Построение Витхоффа из шестиугольных и треугольных мозаик
Подобно однородным многогранникам существует восемь однородных мозаик, базирующихся на правильных шестиугольных мозаиках (или на двойственных треугольных мозаиках).
Если нарисовать плитки исходных граней красным, исходные вершины (получившиеся на их месте многоугольники) жёлтым, а исходные рёбра (получившиеся на их месте многоугольники) синим, существует 8 форм, 7 из которых топологически различны. (Усечённая треугольная мозаика топологически идентична шестиугольной мозаике.)
Связанные правильные комплексные бесконечноугольники
Существует 4 правильных комплексных апейрогона, имеющих те же вершины шестиугольной мозаики. Рёбра правильных комплексных апейрогонов могут содержать 2 и более вершин. Правильные апейрогоны pq>r имеют ограничение: 1/p + 2/q + 1/r = 1. Рёбра имеют p вершин и вершинные фигуры являются r- угольниками .
Первый апейрогон состоит из 2-рёбер, следующие два имеют треугольные рёбра, последний имеет перекрывающиеся шестиугольные рёбра.
Другие треугольные мозаики
Существуют также три мозаики Лавеса, состоящие из треугольников одного типа:
Источник: mobi-scripts.ru
1-2 класс. Узоры из треугольников и Т-паркеты.

Я со всеми хочу на разном уровне позаниматься паркетами.
Поэтому со всеми школьниками мы сегодня играли в очень паркетную игру Тантрикс. Там много всяких вариантов правил, мы по самому простому. Я ее первый раз увидела в антикафе в Калуге. Но мне стало жалко ее покупать за 1500, особенно если учесть, что мне нужно две штуки на покровские группы, поэтому я ее сделала сама, скачав с сайта https://www.twirpx.com/library/spare_time/board_games/. И мы довольно бодро играли, хотя 1-2 классу трудновато было в голове видеть, какие карточки куда подойдут.
Дальше я дала детям скопировать орнамент, состоящий из разных закрашенных треугольничков на пол-клеточки. Первоклашкам попроще, второклашкам посложнее. И все справились. Помнится, три года назад предыдущему поколению это было здорово сложно. А дальше нужно было придумать свой узор.
И дети развернулись, что я их никак не могла остановить.
А потом мы немножко поговорили про паркеты. В частности про паркет из фигурок в виде буквы Т. И делали задание на разделение на буквы Т. Первоклашкам прямо очень сложно было. Только звезды справились. Я поняла, что надо было побольше дать им сначала поиграть и построить самим такие паркеты, а то очень тяжело. Как следует только звезды справились.
Второклашкам дала побольше построить самим, и у них значительно легче пошло.
А еще с первоклашками мы хорошо побегали в Да-Нет. Одна стена была Да, другая Нет. Я говорила какое-то утверждение, и нужно было отвечать бегом.
Например, «Правда ли, что у прямой есть два конца?» или «Правда ли, что острый угол меньше прямого?» С первоклашками сейчас без беготни никуда.
Источник: ahamathsite.com
Презентация на тему Геометрические паркеты
Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных фигур. Гипотеза: количество паркетов из правильных многоугольников бесчисленное множество.
- Главная
- Математика
- Геометрические паркеты




















Слайды презентации
Слайд 1 Геометрическиепаркеты
Выполнила: ученица 9 класса МОУ «Бестужевская общеобразовательная средняя школа»
Ожигина Ольга
Районная

учебно-исследовательская конференция учащихся «Юность Устьи».
Слайд 2 Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных

Гипотеза: количество паркетов из правильных многоугольников бесчисленное множество.
Слайд 3 Слово паркет имеет благородное французское происхождение, которое в средние века

обозначало небольшой парк, немного спустя – часть зала покрытую ковром.
Слайд 4 В толковом словаре Ожегова С. И. паркет – это планки
из твердых пород дерева для покрытия полов, а также само покрытие.

В математике паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют ровно одну общую вершину, либо имеют одну общую сторону. Паркетом называется «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий.
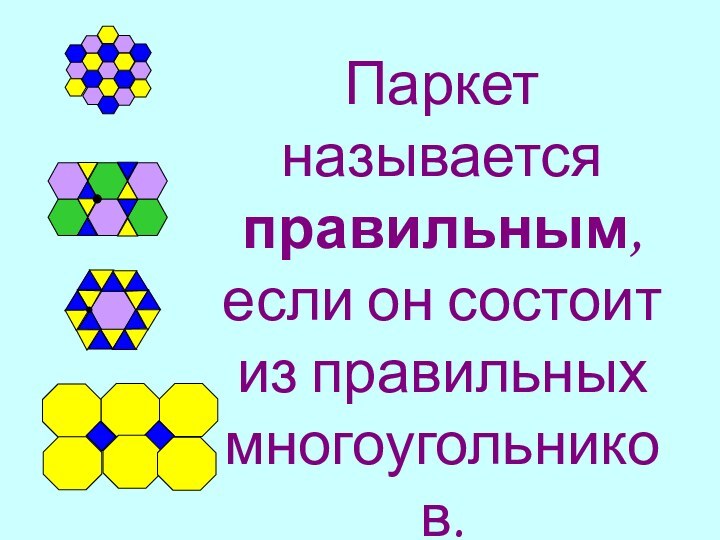
Слайд 5 Паркет называется правильным, если он состоит из правильных многоугольников.

Слайд 6 Паркет из квадратов

Слайд 7 Паркет из шестиугольников.

Слайд 8 Паркет из правильных треугольников.

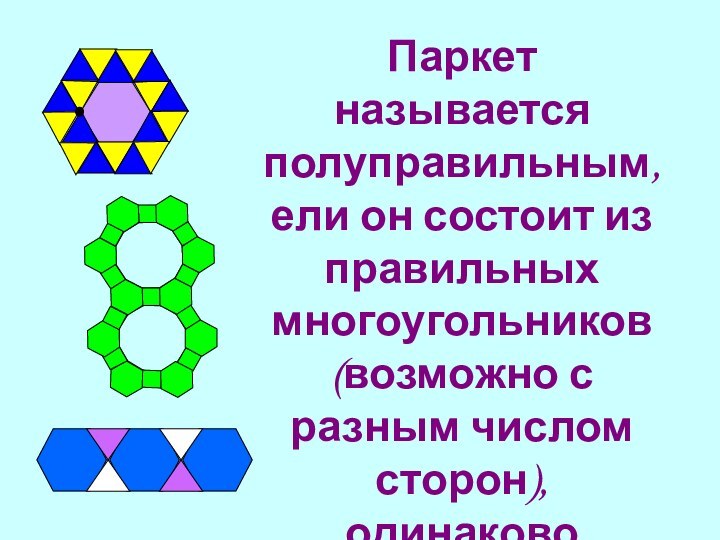
Слайд 9 Паркет называется полуправильным, ели он состоит из правильных многоугольников (возможно

с разным числом сторон), одинаково расположенных вокруг каждой вершины.
Слайд 10 Паркет из шестиугольника и треугольников.

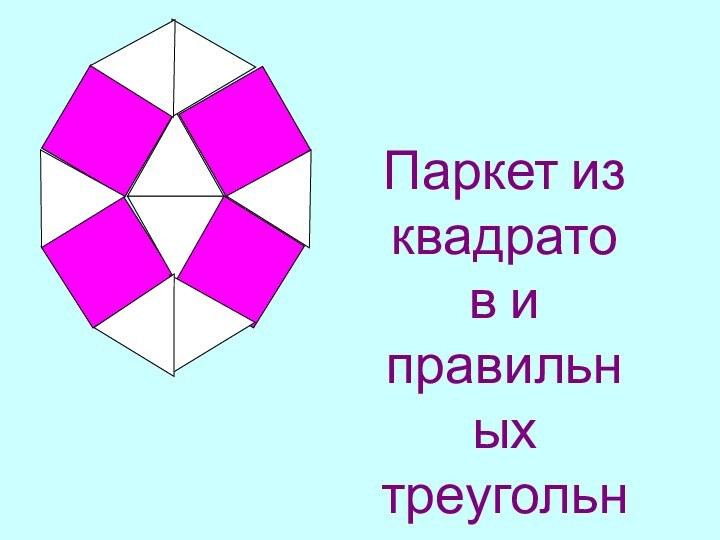
Слайд 11 Паркет из квадратов и правильных треугольников.

Слайд 12 Паркет из квадратов и правильных треугольников.

Слайд 13 Из правильных шестиугольников и треугольников.

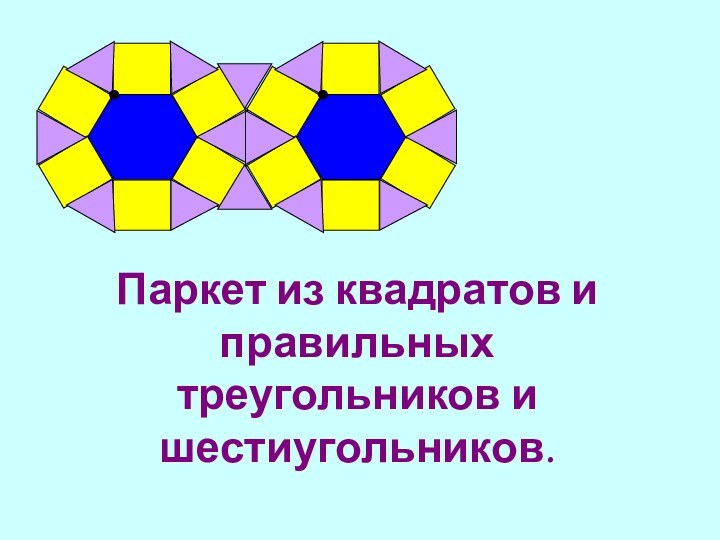
Слайд 14 Паркет из квадратов и правильных треугольников и шестиугольников.

Слайд 15 Паркет из правильных треугольников и двенадцатиугольников.

Слайд 16 Паркет из квадратов, шестиугольников и двенадцатиугольников

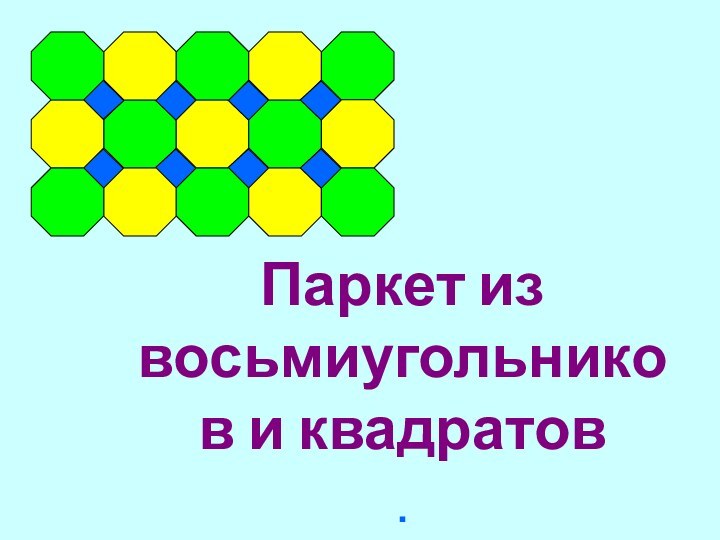
Слайд 17 Паркет из восьмиугольников и квадратов
.

Слайд 18 Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом

называется покрытие плоскости без пропусков и перекрытий заданными фигурами.
Слайд 19 Первый способ.
Паркет, полученный из правильных шестиугольников.

Слайд 20 Второй способ.
Паркет, полученный в результате объединения пяти правильных треугольников.

Слайд 21 Третий способ.
Паркет, полученный объединением паркета из греческих крестов и паркета

из квадратов.
Слайд 22 Четвертый способ.
Паркет, полученный с помощью параллельного переноса

звездчатых многоугольников.
Источник: findtheslide.com