Первый вопрос, который нас интересует и который легко решается, следующий: из каких правильных выпуклых многоугольников можно составить паркет? Ответ на этот вопрос можно найти в задачах о паркетах Пенроуза.
В математике задача сплошного заполнения плоскости многоугольниками без пробелов и перекрытий называется паркетами. Еще древним грекам было известно, что эта задача легко решается при покрытии плоскости правильными треугольниками, квадратами и шестиугольниками.
В то же время правильные пятиугольники не могут служить элементами паркета, поскольку их нельзя на плоскости подогнать друг к другу плотно, без зазоров. То же самое можно сказать о семи-, восьми-, девяти-, десятиугольниках. Постепенно были придуманы способы заполнения плоскости правильными многоугольниками разных видов и размеров. Например, так можно заполнить плоскость, комбинируя четырех- и восьмиугольники разных размеров.
Значительно более сложным развитием этой задачи было условие, чтобы структура паркета, составленного из нескольких видов многоугольников и полностью покрывающего плоскость, была не совсем «правильной» или «почти» периодической. Долгое время считалось, что эта задача не имеет решения. Однако в 60-х годах прошлого столетия она все же была решена, но для этого понадобился набор из тысяч многоугольников различных видов. Шаг за шагом число видов удавалось уменьшить, и, наконец, в середине 1970-х годов профессор Оксфордского университета Роджер Пенроуз решил задачу, используя всего два вида ромбов, заполнения плоскости ромбами с острыми углами в 72 и 36° . Их еще называют «толстыми» и «худыми» ромбами.
Для получения непериодической картины при укладывании ромбов следует придерживаться некоторых нетривиальных правил их сочетания. Оказалось, что эта простая с виду структура обладает очень интересными свойствами. Например, если взять отношение числа тонких ромбов к числу толстых, то оно оказывается всегда равно так называемому «золотому» числу -1,618.
Поскольку это число «не точное», а, как говорят математики, иррациональное, то и структура получается не периодической, а почти периодической. Более того, это число определяет соотношение между отрезками внутри десятиугольников, образующих пятиконечную звезду, — пентограмму, которая считается геометрической фигурой с идеальными пропорциями. Обратите внимание: десятиугольники имеют одинаковую ориентацию, что согласовывает и определяет расположение ромбов, из которых составлена мозаика Пенроуза. Поразительно, что это чисто геометрическое построение оказалось самой подходящей математической моделью для описания открытых в 1984 году квазикристаллов. Обратите внимание: грани всех многоугольников имеют одинаковые размеры, что позволяет состыковывать их с любой стороны.
Глава 2
Классические паркетные узоры (Приложение 1)
Основой для классических паркетных узоров являются прямоугольник, параллелограмм, квадрат, правильные шести и трёх угольники.
Мозаика Пенроуза, бесконечная и неповторимая [Veritasium]
Источник: cyberpedia.su
Презентация на тему Паркеты. Правильные, полуправильные
















Слайд 1 паркеты.
правильные,
полуправильные.

Слайд 2
Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.
паркет

Слайд 3 Из
каких
правильных
многоугольников
можно
составить
паркет?

Слайд 4

Слайд 5
попытка №2 ,
из пятиугольников
увы. ничего не вышло.

Слайд 6

Слайд 7 Необходимое усло-вие для построения паркета.
в
узле
360
градусов
Необходимое усло-вие для построения паркета.

Слайд 8

Слайд 9 теорема №1
Возле любого правильного многоугольника можно описать окружность .
теорема№2
В окружность

можно вписать правильный многоугольник.
Слайд 10 1. при n=3, то m=3600/600=6 треугольников в узле
n=3, то m=3600/600=6 треугольников в узле
2.при n=4 ,то m=3600/900=4 четырёхугольника в узле
3.при.n=5, то т=3600:1080=3.333333
При п>7 внутренние углы правильных п-угольников больше 1200. Кроме того внутренние углы правильного многоугольника всегда меньше1800 .
1200 3600/α > 3600/1800 ,
2 7 не существует правильных многоугольников для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников построить нельзя!

4 . при n=6 , то m=360:120=3 шестиугольника в узле
Слайд 11
Из правильных пятиугольников нельзя сложить паркет.
например:

Слайд 12 вывод:
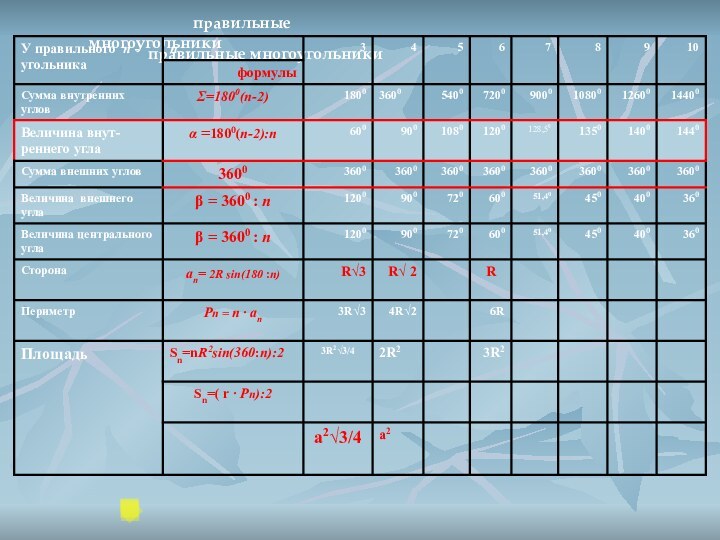
Только из этих правильных многоугольников можно построить правильный паркет.

Слайд 13

Слайд 14

Слайд 15 Необходимое условие для построения паркета.
Необходимое условие для построения паркета.
Источник: findtheslide.com
melnikova_na
Среди огромного разнообразия орнаментов выделяются «паркеты» (мозаики). Паркетом называют заполнение плоскости одинаковыми фигурами (элементами паркета), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда паркетом называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками).
Как известно, на плоскости существуют только три правильных паркета: из правильных треугольников, из квадратов и из правильных шестиугольников. Правильность паркета означает сочетание трёх следующих свойств.
1. У изогонального (вершинно-транзитивного) паркета «равноправны» все вершины. Это значит, что для любых двух вершин существует симметрия паркета, совмещающая первую вершину со второй.
2. У изотоксального (рёберно-транзитивного) паркета «равноправны» все рёбра. Это значит, что для любых двух рёбер существует симметрия паркета, совмещающая первое ребро со вторым.
3. У изоэдрического (гране-транзитивного) паркета «равноправны» все грани. Это значит, что для любых двух граней существует симметрия паркета, совмещающая первую грань со второй.
Под симметрией паркета здесь понимается такое перемещение плоскости, при котором весь паркет точно совмещается сам с собой. Легко убедиться, что сочетание всех трёх свойств возможно только для паркета, состоящего из одинаковых правильных многоугольников.
Паркеты из одинаковых правильных многоугольников:
Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.
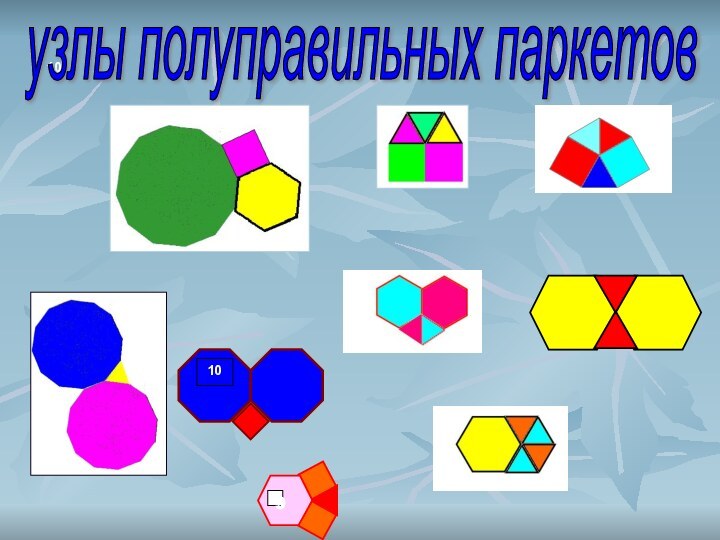
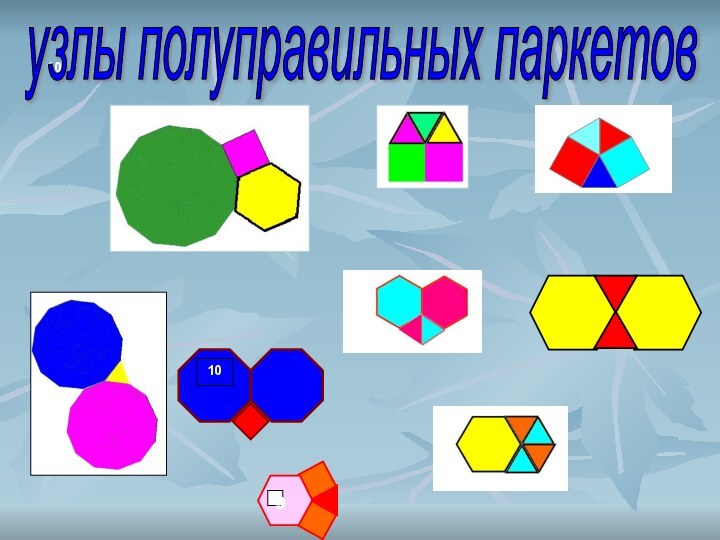
Паркеты из разных правильных многоугольников:
Можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) — два варианта паркета; (3,4,4,6) — четыре варианта; (3,3,3,4,4) — четыре варианта; (3,3,3,3,6); (3,3,3,3,3,3) (цифры в скобках — обозначения многоугольников, сходящихся в каждой вершине: 3 — правильный треугольник, 4 — квадрат, 6 — правильный шестиугольник, 12 — правильный двенадцатиугольник). Некоторые варианты паркета показаны на следующих иллюстрациях:
Паркеты из неправильных многоугольников:
Легко покрыть плоскость параллелограммами:
Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:
Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма.
Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника». В то же время существуют паркеты из невыпуклых семиугольников:
Что изменится если попробовать выложить паркет не на плоской, а на кривой поверхности? Для того чтобы элементы паркета в разных местах поверхности оставались одинаковыми по форме поверхность должна обладать постоянной кривизной. В двумерном случае постоянной отрицательной кривизной обладают гиперболические поверхности, положительной — сферы, а плоскость является промежуточным случаем — поверхностью с постоянной нулевой кривизной.
Прямыми на этих поверхностях являются кратчайшие линии, соединяющие пары точек. На сфере такими линиями являются дуги больших кругов (кругов, плоскости которых проходят через центр сферы). Соответственно, фигуры бывшие на плоскости треугольниками, квадратами и многоугольниками на сфере превращаются в сферические треугольники и многоугольники. Интересной особенностью этих фигур является зависимость суммы углов при их вершинах от размера фигуры (точнее от ее площади). Так у маленького сферического треугольника сумма углов только слегка превышает 180 o , а у треугольника занимающего почти половину сферы она приближается к 360. o
Если взять правильный пятиугольник на сфере, то при определенных размерах его углы станут равными 120 o (а не 108 o , как на плоскости) и три таких пятиугольника будут без зазоров стыковаться друг с другом, если их сложить вершинами. Более того, двенадцать пятиугольников такого размера без зазоров покрывают всю сферу. Эта фигура вам наверняка хорошо известна: некоторое время назад так шили футбольные мячи.
Примеры паркета на поверхности сферы:
Примеры паркета на плоском торе:
Источник: melnikova-na.livejournal.com