Геометрический паркет математика это

Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.

Пифагоровы штаны

Теорема Пифагора для случая равнобедренного прямоугольного треугольника («Наука и жизнь» №9, 2016)

Теорема Пифагора для случая равнобедренного прямоугольного треугольника

Рис. 2. («Наука и жизнь» №9, 2016)

Проверь себя Геометрическая головоломка

Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением * . При чём тут Пифагор?

Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.

4000 лет спустя

История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a 2 + b 2 = c 2 для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a 2 + a 2 = c 2 . Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.

Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия.

И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!

Математическая игротека: паркеты и замощения плоскости.

Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV–III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.

Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.

Иллюстрация к теореме Пифагора из «Трактата об измерительном шесте» (Китай, III век до н. э.) («Наука и жизнь» №9, 2016)

Иллюстрация к теореме Пифагора из «Трактата об измерительном шесте» (Китай, III век до н. э.) и реконструированное на его основе доказательство

Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его. самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!

Первый математик

С. Перкинс. Пифагор («Наука и жизнь» №9, 2016)

С. Перкинс. Пифагор

Пифагора Самосского (570–495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов.

Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.

Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.

Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.

Такое простое доказательство

Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c.

Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a 2 = c · m и b 2 = c · n. Тогда a 2 + b 2 = c · (m + n) = c 2 (рис. 4).

Чертёж к возможному доказательству Пифагора («Наука и жизнь» №9, 2016)

Чертёж к возможному доказательству Пифагора

Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять. Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.

Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны.

Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.

Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.

Мозаика Пифагора

«Мозаика Пифагора» и разбиение ан-Найризи трёх квадратов в доказательстве теоремы Пифагора («Наука и жизнь» №9, 2016)

«Мозаика Пифагора» и разбиение ан-Найризи трёх квадратов в доказательстве теоремы Пифагора

Если покрыть плоскость квадратами двух разных размеров, окружив каждый малый квадрат четырьмя большими, получится паркет «мозаика Пифагора». Такой рисунок издавна украшает каменные полы, напоминая о древних доказательствах теоремы Пифагора (отсюда его название).

По-разному накладывая на паркет квадратную сетку, можно получить разбиения квадратов, построенных на сторонах прямоугольного треугольника, которые предлагались разными математиками. Например, если расположить сетку так, чтобы все её узлы совпали с правыми верхними вершинами малых квадратов, проявятся фрагменты чертежа к доказательству средневекового персидского математика ан-Найризи, которое он поместил в комментариях к «Началам» Евклида. Легко видеть, что сумма площадей большого и малого квадратов, исходных элементов паркета, равна площади одного квадрата наложенной на него сетки. А это означает, что указанное разбиение действительно пригодно для укладки паркета: соединяя в квадраты полученные многоугольники, как показано на рисунке, можно заполнить ими без пробелов и перекрытий всю плоскость.

П. де Хох. Хозяйка и служанка во внутреннем дворике; Я. Охтервелт. Бродячие музыканты в дверях богатого дома («Наука и жизнь» №9, 2016)

Правильный паркет из квадратов и «мозаика Пифагора» на картинах голландских мастеров. Слева: П. де Хох. Хозяйка и служанка во внутреннем дворике. Около 1660 года. Справа: Я. Охтервелт.

Бродячие музыканты в дверях богатого дома. 1665 год

* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.

Источник: elementy.ru

Презентация на тему Геометрические паркеты

Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных фигур. Гипотеза: количество паркетов из правильных многоугольников бесчисленное множество.

Главная
Математика
Геометрические паркеты

ГеометрическиепаркетыВыполнила: ученица 9 класса МОУ «Бестужевская общеобразовательная средняя школа»Ожигина ОльгаРайонная учебно-исследовательская конференция учащихся «Юность Устьи». Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных фигур. Гипотеза: Слово паркет имеет благородное французское происхождение, которое в средние века обозначало небольшой В толковом словаре Ожегова С. И. паркет – это планки из твердых Паркет называется правильным, если он состоит из правильных многоугольников. Паркет из квадратов Паркет из шестиугольников. Паркет из правильных треугольников. Паркет называется полуправильным, ели он состоит из правильных многоугольников (возможно с разным Паркет из шестиугольника и треугольников. Паркет из квадратов и правильных треугольников. Из правильных шестиугольников и треугольников. Паркет из правильных треугольников и двенадцатиугольников. Паркет из квадратов, шестиугольников и двенадцатиугольников Паркет из восьмиугольников и квадратов. Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие Первый способ.Паркет, полученный из правильных шестиугольников. Второй способ.Паркет, полученный в результате объединения пяти правильных треугольников. Третий способ.Паркет, полученный объединением паркета из греческих крестов и паркета из квадратов. Четвертый способ.Паркет, полученный с помощью параллельного переноса звездчатых многоугольников. Паркеты, придуманные мной. Спасибо за внимание!

Слайды презентации

Слайд 1 Геометрическиепаркеты
Выполнила: ученица 9 класса МОУ «Бестужевская общеобразовательная средняя школа»
Ожигина Ольга
Районная

учебно-исследовательская конференция учащихся «Юность Устьи».

Слайд 2 Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных

Цель: подробно изучить паркеты из многоугольников, правильных многоугольников и произвольных фигур.

Гипотеза: количество паркетов из правильных многоугольников бесчисленное множество.

Слайд 3 Слово паркет имеет благородное французское происхождение, которое в средние века

Слово паркет имеет благородное французское происхождение, которое в средние века обозначало

обозначало небольшой парк, немного спустя – часть зала покрытую ковром.

Слайд 4 В толковом словаре Ожегова С. И. паркет – это планки

из твердых пород дерева для покрытия полов, а также само покрытие.

В толковом словаре Ожегова С. И. паркет – это планки из

В математике паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют ровно одну общую вершину, либо имеют одну общую сторону. Паркетом называется «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий.

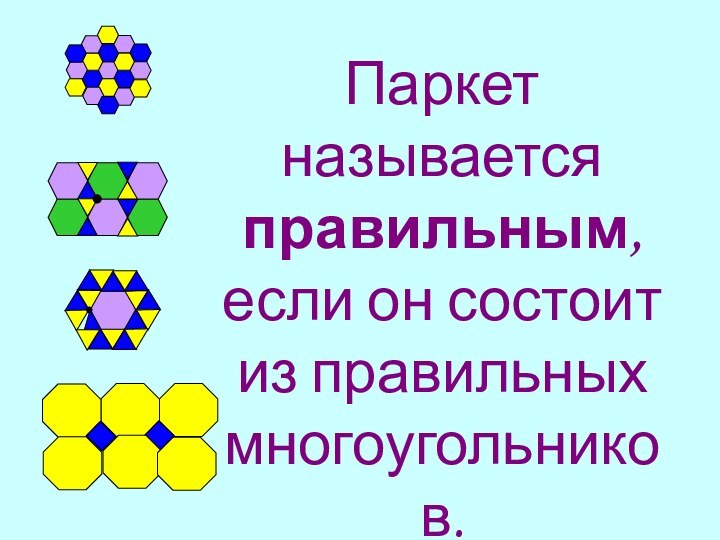
Слайд 5 Паркет называется правильным, если он состоит из правильных многоугольников.

Паркет называется правильным, если он состоит из правильных многоугольников.

Слайд 6 Паркет из квадратов

Паркет из квадратов

Слайд 7 Паркет из шестиугольников.

Паркет из шестиугольников.

Слайд 8 Паркет из правильных треугольников.

Паркет из правильных треугольников.

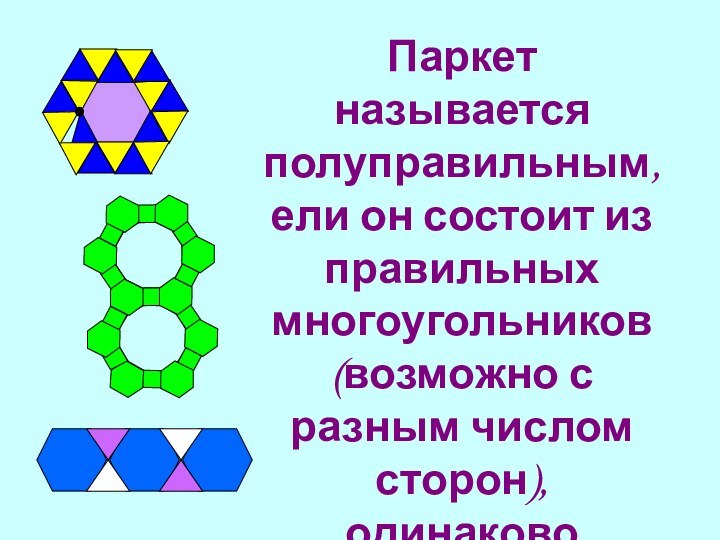
Слайд 9 Паркет называется полуправильным, ели он состоит из правильных многоугольников (возможно

Паркет называется полуправильным, ели он состоит из правильных многоугольников (возможно с

с разным числом сторон), одинаково расположенных вокруг каждой вершины.

Слайд 10 Паркет из шестиугольника и треугольников.

Паркет из шестиугольника и треугольников.

Слайд 11

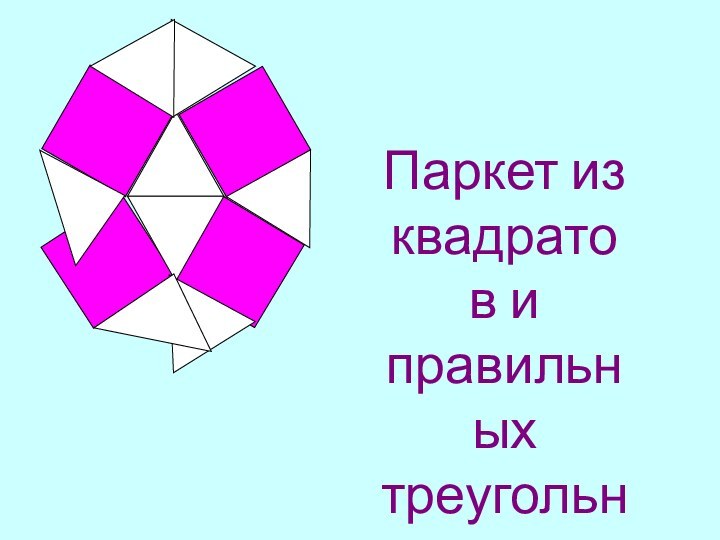
Паркет из квадратов и правильных треугольников.

Слайд 12 Паркет из квадратов и правильных треугольников.

Паркет из квадратов и правильных треугольников.

Слайд 13 Из правильных шестиугольников и треугольников.

Из правильных шестиугольников и треугольников.

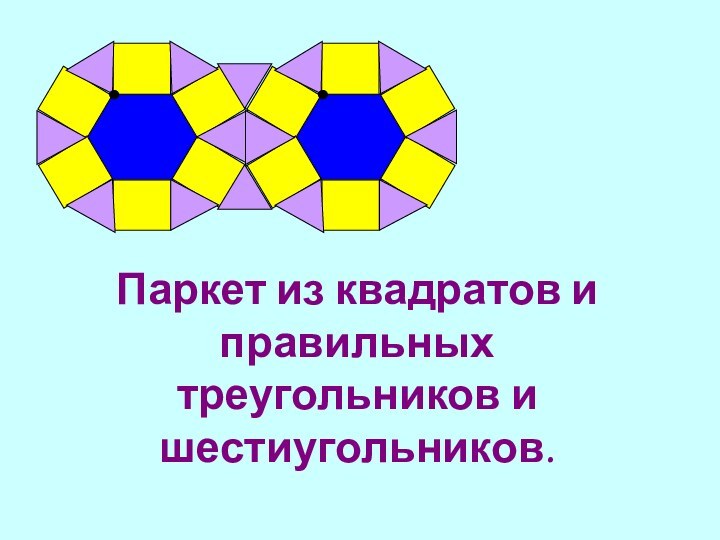
Слайд 14 Паркет из квадратов и правильных треугольников и шестиугольников.

Паркет из квадратов и правильных треугольников и шестиугольников.

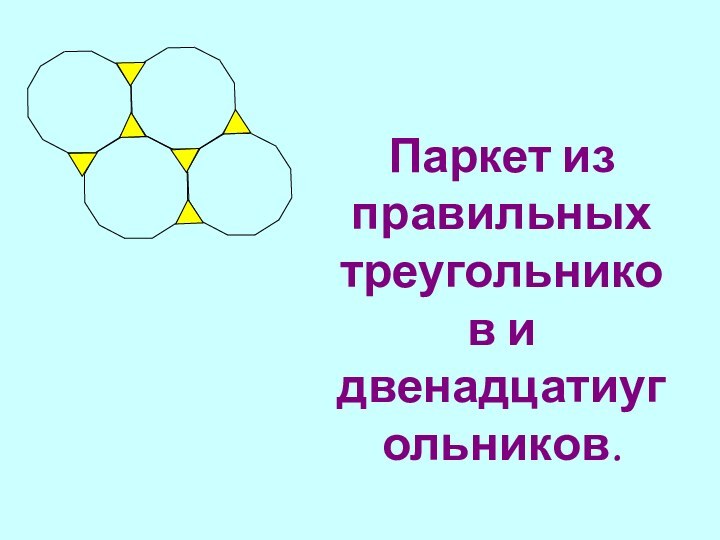
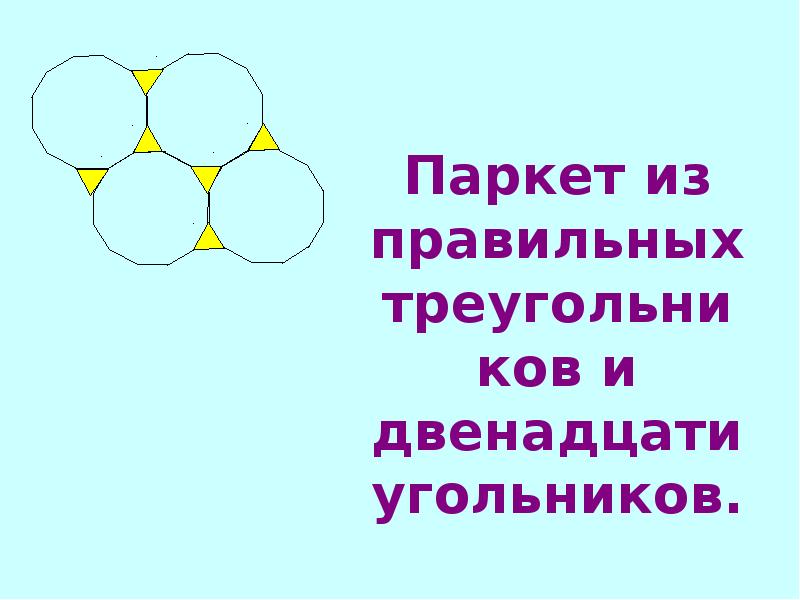
Слайд 15 Паркет из правильных треугольников и двенадцатиугольников.

Паркет из правильных треугольников и двенадцатиугольников.

Слайд 16 Паркет из квадратов, шестиугольников и двенадцатиугольников

Паркет из квадратов, шестиугольников и двенадцатиугольников

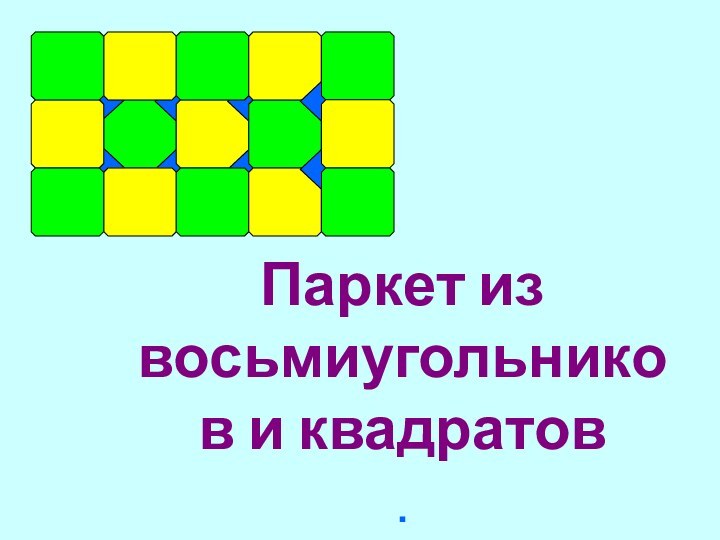
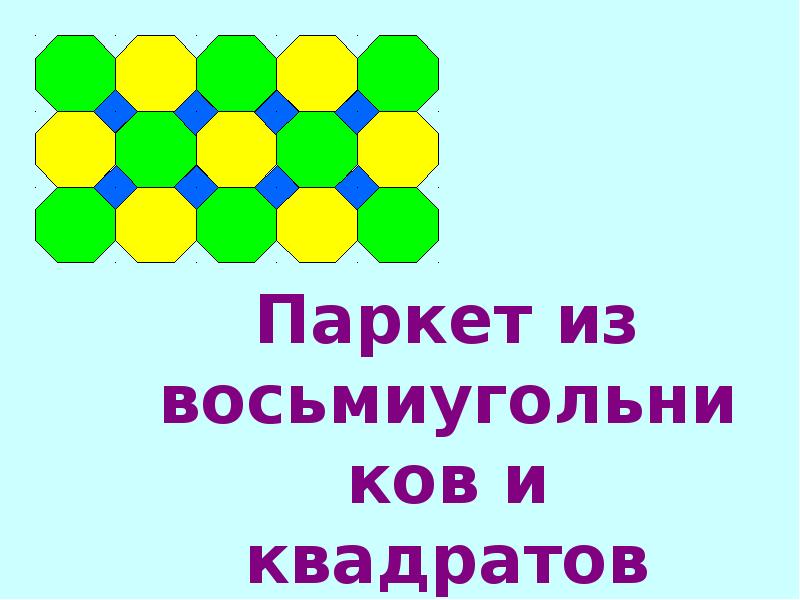
Слайд 17 Паркет из восьмиугольников и квадратов
.

Паркет из восьмиугольников и квадратов.

Слайд 18 Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом

Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется

называется покрытие плоскости без пропусков и перекрытий заданными фигурами.

Слайд 19
Первый способ.

Паркет, полученный из правильных шестиугольников.

Первый способ.Паркет, полученный из правильных шестиугольников.

Слайд 20 Второй способ.
Паркет, полученный в результате объединения пяти правильных треугольников.

Второй способ.Паркет, полученный в результате объединения пяти правильных треугольников.

Слайд 21 Третий способ.
Паркет, полученный объединением паркета из греческих крестов и паркета

Третий способ.Паркет, полученный объединением паркета из греческих крестов и паркета из квадратов.

из квадратов.

Слайд 22 Четвертый способ.
Паркет, полученный с помощью параллельного переноса

Четвертый способ.Паркет, полученный с помощью параллельного переноса звездчатых многоугольников.

звездчатых многоугольников.

Источник: findtheslide.com

Презентация на тему Геометрические паркеты

Вы можете изучить и скачать доклад-презентацию на тему Геометрические паркеты. Презентация на заданную тему содержит 25 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации » Математика » Презентация Геометрические паркеты

Геометрическиепаркеты Выполнила: ученица 9 класса МОУ «Бестужевская общеобразовательная средняя школа» Ожигина