Упражнения 371 — 398 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 2. Параллелограмм и трапеция (43. Параллелограмм. 44. Признаки параллелограмма. 45.
Трапеция). Геометрия 8 класс Атанасян Задачи 371-398 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 2. Параллелограмм и трапеция
Задачи №№ 371 — 398:
Задача № 371. □ Докажите, что выпуклый четырёхугольник ABCD является параллелограммом, если: a) ∠BAC = ∠ACD и ∠BCA = ∠DАС; б) АВ||CD, ∠A = ∠C. .
Смотреть решение задачи № 371

Задача № 372. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если: а) одна сторона на 3 см больше другой; б) разность двух сторон равна 7 см; в) одна из сторон в два раза больше другой. .
Смотреть решение задачи № 372

№ 392 — Геометрия 7-9 класс Атанасян
Задача № 373. Периметр параллелограмма ABCD равен 50 см, ∠C = 30°, а перпендикуляр ВН к прямой CD равен 6,5 см. Найдите стороны параллелограмма. .
Смотреть решение задачи № 373

Задача № 374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр этого параллелограмма, если ВК = 15 см, КС = 9 см.
Смотреть решение задачи № 374

Задача № 375. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. .
Смотреть решение задачи № 375

Задача № 376. Найдите углы параллелограмм: ABCD, если: a) ∠A = 84°; б) ∠A – ∠B = 55°; в) ∠A + ∠C = 142°; г) ∠А = 2∠В; д) ∠CAD = 16°, ∠ACD = 37°. .
Смотреть решение задачи № 376

Задача № 377. В параллелограмме MNPQ проведён перпендикуляр NH к прямой MQ, причём точка Н лежит на стороне MQ. Найдите стороны и углы параллелограмма, если известно, что МН = 3 см, HQ = 5 см, ∠MNH = 30°. .
Смотреть решение задачи № 377

Задача № 378. Докажите, что параллелограмм является выпуклым четырёхугольником .
Смотреть решение задачи № 378

Задача № 379. □ Из вершин В и D параллелограмма ABCD, у которого АВ ≠ ВС и угол А острый, проведены перпендикуляры ВК и DM к прямой АС. Докажите, что четырёхугольник BMDK — параллелограмм. .
Смотреть решение задачи № 379
№261. Докажите, что в равнобедренном треугольнике высоты, проведенные из вершин основания, равны.

Задача № 380. На сторонах АВ, ВС, CD и DA четырёхугольника ABCD отмечены соответственно точки М, N, Р и Q так, что АМ = СР, BN = DQ, BM = DP, NC = QA. Докажите, что ABCD и MNPQ — параллелограммы. .
Смотреть решение задачи № 380

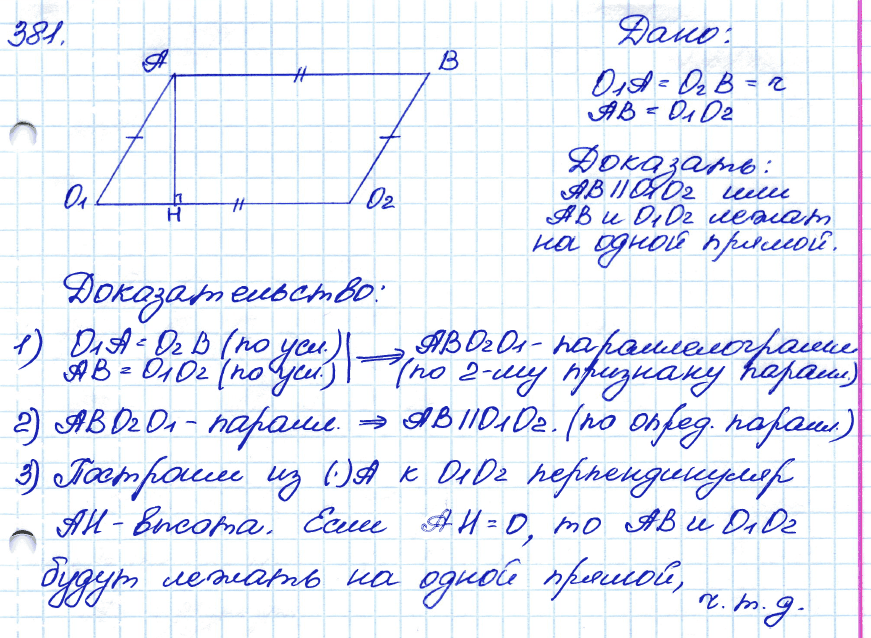
Задача № 381. На рисунке 163 изображены два одинаковых колеса тепловоза. Радиусы О1А и О2В равны. Стержень АВ, длина которого равна расстоянию О1О2 между центрами колёс, передаёт движение от одного колеса к другому. Докажите, что отрезки АВ и О1О2 либо параллельны, либо лежат на одной прямой. .
Смотреть решение задачи № 381
Задача № 382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырёхугольник A1B1C1D1, вершинами которого являются середины отрезков ОА, ОВ, ОС и OD, — параллелограмм. .
Смотреть решение задачи № 382

Задача № 383. На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что РВ = QD. Докажите, что четырёхугольник APCQ — параллелограмм. .
Смотреть решение задачи № 383

Задача № 384. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.
Смотреть решение задачи № 384

Задача № 385. Докажите теорему Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Смотреть решение задачи № 385

Задача № 386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. .
Смотреть решение задачи № 386

Задача № 387. Найдите углы В и D трапеции ABCD с основаниями AD и ВС, если ∠A = 36°, ∠C =117°. .
Смотреть решение задачи № 387

Задача № 388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равны; б) диагонали равны. .
Смотреть решение задачи № 388

Задача № 389. Докажите, что трапеция равнобедренная, если: а) углы при основании равны; б) диагонали трапеции равны. .
Смотреть решение задачи № 389

Задача № 390. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции. .
Смотреть решение задачи № 390

Задача № 391. Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости. .
Смотреть решение задачи № 391

Задача № 392. □ Основания прямоугольной трапеции равны а и b, один из углов равен α. Найдите: а) большую боковую сторону трапеции, если а = 4см, b = 7см, α = 60°; б) меньшую боковую сторону трапеции, если а = 10 см, b = 15 см, α = 45°. .
Смотреть решение задачи № 392

Задача № 393. □ Постройте параллелограмм: а) по двум смежным сторонам и углу между ними; б) по двум диагоналям и углу между ними; в) по двум смежным сторонам и соединяющей их концы диагонали.
Смотреть решение задачи № 393

Задача № 394. Даны три точки А, B и С, не лежащие на одной прямой. Постройте параллелограмм так, чтобы три его вершины совпадали с данными точками. Сколько таких параллелограммов можно построить? .
Смотреть решение задачи № 394

Задача № 395. Даны острый угол hk и два отрезка P1Q1 и P2Q2. Постройте параллелограмм ABCD так, чтобы расстояние между параллельными прямыми АВ и DC равнялось P1Q1, AB = P2Q2 и ∠A = ∠hk.
Смотреть решение задачи № 395

Задача № 396. Разделите данный отрезок АВ на п равных частей
Смотреть решение задачи № 396

Задача № 397. □ Постройте равнобедренную трапецию ABCD: а) по основанию AD, углу А и боковой стороне АВ; б) по основанию ВС, боковой стороне АВ и диагонали BD.
Смотреть решение задачи № 397

Задача № 398. □ Постройте прямоугольную трапецию ABCD по основаниям и боковой стороне AD, перпендикулярной к основаниям.
Смотреть решение задачи № 398

Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 2. Параллелограмм и трапеция. Геометрия 8 класс Атанасян Задачи 371-398 + ОТВЕТЫ.
Источник: xn--8-8sb3ae5aa.xn--p1ai
Гдз по геометрии 7-9 класс Атанасян, Бутузов ответ на номер № 391

Подробный решебник (ГДЗ) по Геометрии за 7‐9 (седьмой‐девятый) класс — готовый ответ номер — 391. Авторы учебника: Атанасян, Бутузов, Кадомцев, Позняк, Юдин. Издательство: Просвещение 2016.
Похожие ГДЗ

ГДЗ Рабочая тетрадь геометрия 8 класс Л.С. Атанасян

ГДЗ Рабочая тетрадь геометрия 9 класс Л.С. Атанасян

ГДЗ Рабочая тетрадь геометрия 7 класс Л.С. Атанасян
Условие / номер / 391
391 Докажите, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости.
Источник: megaresheba.ru
Докажите что из одинаковых плиток имеющих форму равнобедренной трапеции можно сделать паркет 8 класс

XI Международный конкурс научно-исследовательских и творческих работ учащихся
Старт в науке
- Главная
- Список секций
- Математика
- Применение теории паркетов для доказательства признаков параллелограмма и трапеции.



Применение теории паркетов для доказательства признаков параллелограмма и трапеции.
Рампилова С.А. 1
1 МБОУ «Кижингинский лицей имени В. С. Мункина»
Степанова Т.Ц. 1
1 МБОУ «Кижингинский лицей имени В. С. Мункина»

Автор работы награжден дипломом победителя II степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Тема «Четырехугольники» является основной и интереснейшей в курсе восьмого класса. При её изучении рассматриваются важнейшие свойства трапеции, параллелограмма и его частных видов – прямоугольника, ромба, квадрата.
Однако при решении задач, прежде чем воспользоваться теоремой-свойством, необходимо доказать, что данная фигура относится к определенному виду. Для этого даны теоремы-признаки.
В школьном учебнике Л. С. Атанасян «Геометрия 7-9» рассмотрены три признака параллелограмма и нет признаков для трапеции. Поэтому знание признаков указанных четырехугольников необходимо.
Цель исследования – изучение признаков параллелограмма и трапеции.
Актуальность данной работы: В курсе геометрии 8 класса есть задача 391 условием задачи было доказать, что из одинаковых плиток, имеющих форму равнобедренной трапеции, можно сделать паркет, полностью покрывающий любую часть плоскости. Решая эту задачу, я задумалась над применением теории паркетов. Изучала материалы в Интернет-ресурсах и специальной литературе.
Объект исследования: Четырехугольники.
Предмет исследования: Свойства и признаки четырехугольника.
Методы исследования: изучение и анализ литературы по данной теме, также Интернет-ресурсов и экспериментальная проверка некоторых фактов.
Практическая значимость исследования: Расширение знаний и кругозора учащихся, использование материалов (задач) на уроках геометрии.
Теорема-признак формулируется как обратное утверждение свойству. Поэтому, группируя по два свойства параллелограмма (аналогично для трапеции) и составляя обратные теоремы, я либо доказывала их, либо опровергала с помощью контр-прим
Однако, таким образом я не исчерпала всего множества признаков параллелограмма и трапеции. Это было мною осознанно при решении задачи: четырехугольником произвольной формы заполнить всю пропусков и перекрытий.
Задачи замощения плоскости дают возможность доказать ранее не выявленные нами свойства и признаки параллелограмма и трапеции.
Использование теории паркета для решения вопроса – сколько всего признаков у параллелограмма и трапеции – позволили сформулировать тему исследования:
«Применение теории паркета для доказательства свойств и признаков трапеции и параллелограмма».
Свойства и признаки параллелограмма и трапеции.
1)AB || CD
2)BC || AD
3)AB = CD
4)BC = AD
5)AO = OC
6)BO = OD
7)∠A = ∠C
8)∠B = ∠D
9) ∠A + ∠B = 180°
10) ∠B + ∠C = 180°
11) ∠C + ∠D = 180°
12) ∠D + ∠A = 180°
Одного свойства не достаточно для составления признака, а три — избыточно. Поэтому сочетая по два свойства, составим обратные теоремы и проверим их на истинность. В таблице попарно сгруппированы все 12 свойств. Одинаковым цветом выделены свойства, формирующие схожие признаки. Черным те которые не удовлетворяют требованиям.
Приведем доказательства этих признаков, а также контр-примеры для неверных признаков.
Если в выпуклом четырехугольнике сумма длин средних линий равна его полупериметру, то этот четырехугольник параллелограмм.
Равенство в обоих случаях выполняется, когда AB || CD и BC || AD . Поусловию MN + KH = ½ (AB + CD + BC + AD) = ½ (AB + CD) + ½ (BC + AD). Следовательно , MN = ½ (AB + CD) и KH = ½ (BC + AD). Итак , AB || CD и BC || AD → ABCD – параллелограмм .
Изображена таблица, полученная при парной группировке свойств трапеции.
Задача о построении паркета из четырехугольника.
Задача: четырехугольником произвольной формы настлать паркет, то есть заполнить всю плоскость без пропусков и перекрытий. Решение этой задачи можно получить с помощью центральной симметрии. Отразим четырехугольник ABCD симметрично относительно середины стороны AB . На рисунке исходный четырехугольник помечен цифрой 1, а симметричный – цифрой 2. Теперь 2-ой отразим симметрично относительно середины его стороны BC , а полученный четырехугольник 3 – относительно середины его стороны CB . Четырехугольники 1, 2, 3, 4 примыкают к их общей вершине углами A , B , C , D . А так как сумма углов в четырехугольнике равна 360˚, то эти четыре четырехугольника располагаются вокруг их общей вершины без пропусков и перекрытий. Такое же построение провести вокруг каждой вершины каждого из новых четырехугольников, что и дает паркет на всей плоскости.
Закрасим четырехугольники в два цвета. В раскрашенном таким образом паркете два четырехугольника одного цвета получаются друг из друга параллельным переносом, а два четырехугольника разных цветов – центральной симметрией. Заметим что исходный четырехугольник может быть и не выпуклым – паркет получится и в этом случае.
Примеры решения задач с использованием паркетов.
Построенные паркеты позволяют решить ряд задач, связанных со свойствами четырехугольников. Решение задач можно изложить без использования паркета; рассмотреть только те четырехугольники, которые нужны для решения, а остальные «следы» паркета стереть. Однако найти решение проще с использованием паркета.
Из бумаги изготовили два одинаковых выпуклых четырехугольника. Один разрезали по одной диагонали, второй – по другой. Докажите, что из четырех полученных треугольников можно составить параллелограмм. Решение становиться очевидным при рассмотрении паркета, изображенного на рисунке.
Докажите, что паркет из четырехугольников можно получить следующим образам: застилается паркет из центрально-симметричных шестиугольников (произвольной формы, даже не выпуклых) так, что любые два шестиугольника получаются друг из друга параллельным переносом.
На рисунке, а изображен центрально-симметричный шестиугольник ABCDEF . Другие шестиугольники получены из него параллельным переносом. Сумма внутренних углов шестиугольника, рассчитанная по формуле ( n -2)×180˚, равна 720˚. Угол A = D , B = E , C = F , так как по условию задачи шестиугольник центрально-симметричен. Следовательно, сумма углов B , D . F , прилегающих в общей вершине, равна 360˚, а значит, три этих шестиугольника расположены вокруг нее без пропусков и перекрытий. Далее, проводят параллельные диагонали, они образуют параллелограммы и не нарушают паркет.
Применение теории паркета для доказательства свойств и признаков параллелограмма и трапеции.
Докажите, что если средняя линия, соединяющая середины двух противоположных сторон четырехугольника, равна полу-сумме двух других противоположных сторон, то это четырехугольник – трапеция(или параллелограмм).
На рисунке MN и NP – средние линии; отрезки AQ и MP равны и параллельны (поскольку AM и QP равны и параллельны). Если MP = 1/3 ( AB + BQ ), то есть AQ = MP = AB + BQ , то точка B принадлежит отрезку AQ . Следовательно, AB || CB , то есть ABCD – трапеция.
Существует ещё одно свойство параллелограмма: любой отрезок, соединяющий две противоположные стороны параллелограмма и проходящий через точку пересечения диагоналей, разделится ею по полам. Связанно это с тем, что параллелограмм обладает центральной симметрией, и его центр симметрии и его центр находится в точке пересечения диагоналей.
Обратная теорема: если любой отрезок с концами на сторонах четырехугольника в точке пересечения диагоналей делится пополам, то этот четырехугольник – параллелограмм.
На рисунке отрезок PK соединяет две противоположные стороны четырехугольника через точку пересечения диагоналей и делится ею пополам. Соединим точку O ₂ — точку пересечения диагоналей и точку P ₁, а также и точку O ₁ c P ₂. Получим ромб O ₁ P ₁ O ₂ P ₂ с диагональю O ₂ O ₁ и P ₂ P ₁. Известно, что диагонали ромба взаимно перпендикулярны. Значит, O ₂ H ₁, который в равнобедренном треугольнике NO ₂ K ₂ будет является медианой и высотой.
Аналогично доказывается параллельность сторон A ₂ D ₂ || B ₂ C ₂ → ABCD – параллелограмм.
Доказать, что если в трапеции диагонали равны, то она равнобедренная.
На рисунке A ₂ C ₂ B ₁ B ₂ — ромб (поскольку его стороны равны и параллельны). Так как диагонали ромба перпендикулярны и делятся точкой пересечения пополам, то отрезок BP – медиана и высота в треугольнике ABD ₁. Следовательно, ∆ ABD ₁ — равнобедренный → AB = C ₁ D ₁.
Начатая мной работа по отысканию признаков параллелограмма и трапеции ещё не завершена. Для составления теорем-признаков необходимо знать все свойства параллелограмма и трапеции, многие из которых остались за рамками школьной программы. Не до конца использована мной теория паркетов для доказательства свойств и признаков параллелограмма и трапеции. (Эта идея почерпнута мной из статьи «Паркет из четырехугольников» — автор – доктор – математических наук В. Г. Болотянский.)
Во всем этом я видим перспективы данного исследования. Однако уже на данном этапе работы мне многое удалось.
Во-первых, мной рассмотрена задача о «замощении» плоскости четырехугольниками.
Во-вторых, пополнены «школьные» признаки параллелограмма и трапеции.
В-третьих, доказаны признаки параллелограмма и трапеции, обратные свойствам их средней линии.
В-четвертых, открыт «новый способ» доказательства признаков параллелограмма и трапеции.
Атанасян, Л. С. Геометрия [Текст]: учебник. для 7-9 кл. сред. шк. / Л. С. Атанасян, В. Ф. Бутузов. – М.: Просвещение, 1991.
Болтянский, В. Г. Паркет из четырехугольников. [Текст] / В. Г. Болтянский // Квант. – М.: Наука. – 1989. – №11.
Готман, Э. Задачи на доказательство. [Текст] / Э. Готман // Квант. – М.: Наука. – 1976. – №7
Готман, Э. Медианы и средним линии. [Текст] / Э. Готман // Квант. – М.: Наука. – 1975. – №12
Кушнир, И. Неожиданность обратной задачи. [Текст] / И. Кушнир // Квант. – М.: Наука. – 1991. – №2
Математика. [Текст] // Энциклопедия для детей. – Т. 11. – Аванта+, 1998.
Погорелов, А. В. Геометрия. [Текст]: учеб. пособие для 6-10 кл. сред. шк. / А. В. Погорелов. – М.: Просвещение, 1998.
Сонин, А. С. Постижение совершенства [Текст] / А. С. Сонин. – М., 1986.
Источник: school-science.ru