Парке́т — замощение плоскости многоугольниками без пробелов и перекрытий, в котором любые два многоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек.
Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов —выпуклых пятиугольников, которыми можно замостить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад. Об этом сообщает издание The Guardian.
Нет, на фото это конечно не он. Вот про него подробее …
Проблема нахождения и классификации паркетных многоугольников является одной из наиболее актуальных в современной комбинаторной геометрии. Известно, что любым треугольником и четырехугольником можно замостить плоскость, а также то, что существуют только три типа выпуклых шестиугольников, способных выполнить такую же задачу.
Фигурами, имеющими более шести сторон, замостить плоскость невозможно. Математикам в настоящее время не известно точное число типов пятиугольников, способных замостить плоскость.
9 класс, 22 урок, Окружность, описанная около правильного многоугольника
Первую классификацию таких пятиугольников осуществил к 1918 году математик Карен Рейнхард, описавший пять типов фигур. В период с 1968 по 1985 год четырьмя другими учеными были найдены еще девять типов аналогичных многоугольников. Открытие американскими учеными 15-го типа пятиугольников стало первым за последние 30 лет.
«Проблема классификации выпуклых пятиугольников, которыми можно замостить плоскость, является красивой и достаточно простой математической задачей, доступной для понимания даже детям. Эта проблема уже в течение ста лет не имеет полного решения», — сказал один из открывших 15-й тип выпуклого пятиугольника математик Кейси Манн. Он же отметил связь этой задачи с 18-й проблемой Гильберта.
Манн также отметил, что пока не знает, найдут ли он и его коллеги новые типы пятиугольников, которые могут замостить плоскость. С этой целью математики собираются продолжить свои исследования, представляющие собой перебор на компьютере существующих возможностей.
Как замечает Манн, исследование пятиугольных фигур представляет не только академический, но и практический интерес. «Многие структуры, которые мы видим в природе, например капсиды вирусов, состоят из специальным образом формирующих свою геометрию и динамику строительных блоков, объединяющихся вместе для формирования структуры большего масштаба», — говорит математик.
Источник: masterok.livejournal.com
Презентация, доклад по математике на темуПаркет
ВведениеЦель: составление паркета с помощью различных геометрических фигур.Задачи: Изучить литературу, интернет-ресурсы по заданной теме. Закрепить знания свойств правильных многоугольников в процессе исследования вопроса о покрытии плоскости правильными многоугольниками.Обосновать с помощью математических фактов, как можно уложить паркет.определить
Геометрия 9 класс (Урок№26 — Построение правильных многоугольников.)
- Главная
- Математика
- Презентация по математике на темуПаркет
Слайд 1Исследовательская работа по теме:
«Паркет из многоугольников»
Выполнил : Лобачев Павел, ученик 9А
класса МБОУ «Инсарская СОШ №2» Руководитель: Кузнецова О. Г., учитель математики «Инсарская СОШ №2»
МБОУ «Инсарская СОШ №2»

Слайд 2Введение
Цель: составление паркета с помощью различных геометрических фигур.
Задачи:
Изучить литературу, интернет-ресурсы
по заданной теме.
Закрепить знания свойств правильных многоугольников в процессе исследования вопроса о покрытии плоскости правильными многоугольниками.
Обосновать с помощью математических фактов, как можно уложить паркет.
определить количество правильных и полуправильных паркетов.
Объект исследования : паркеты.
Методы исследования: анализ научной, учебной литературы; сравнение и анализ результатов, полученных разными авторами; их систематизация; метод аналогии.

Слайд 3Что такое паркет?

Слайд 4
В геометрии паркетом называется разбиение плоскости многоугольниками, при котором каждые два многоугольника
либо не пересекаются, либо имеют одну общую вершину, либо имеют общую сторону.

Слайд 5 Правильный многоугольник — это выпуклый многоугольник, у которого все углы равны
и все стороны равны.
Паркеты из правильных многоугольников
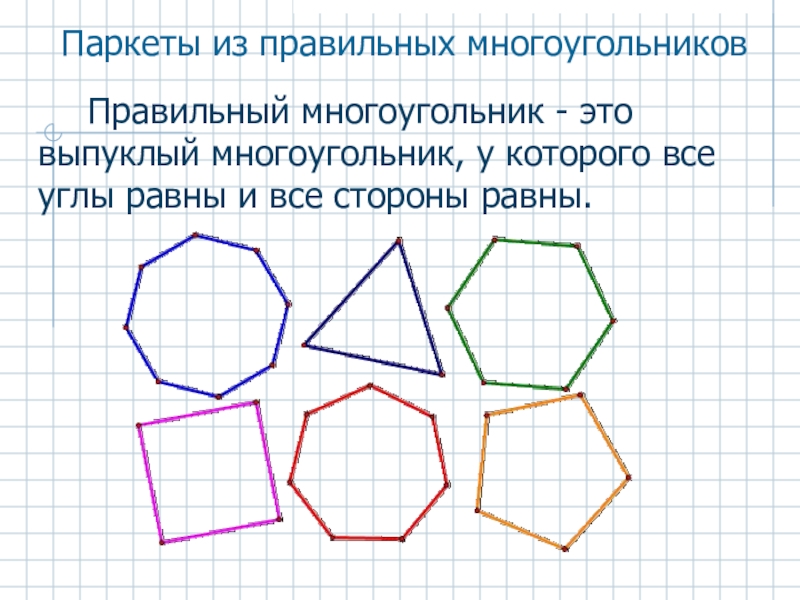
Слайд 6Градусная мера угла правильного многоугольника:
αn=((n-2)*180)/n
360n/((n-2)*180)=m, где m–целое число, показывающее
кол-во многоугольников.
Решая уравнение, получаем: n1=3, m1=6; n2=4,m2=4; n3=6,m3=3.
Это означает, что замостить плоскость вокруг точки можно при помощи правильных многоугольников: шести треугольников, четырёх квадратов и трёх шестиугольников.
Слайд 7 Если при составлении паркета использовалось несколько правильных
многоугольников с различным числом сторон, то такой паркет называется полуправильным.
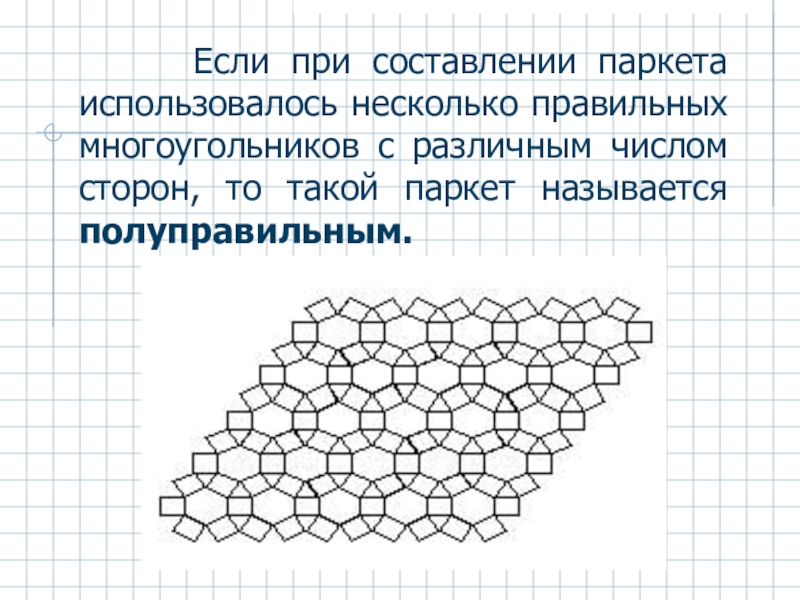
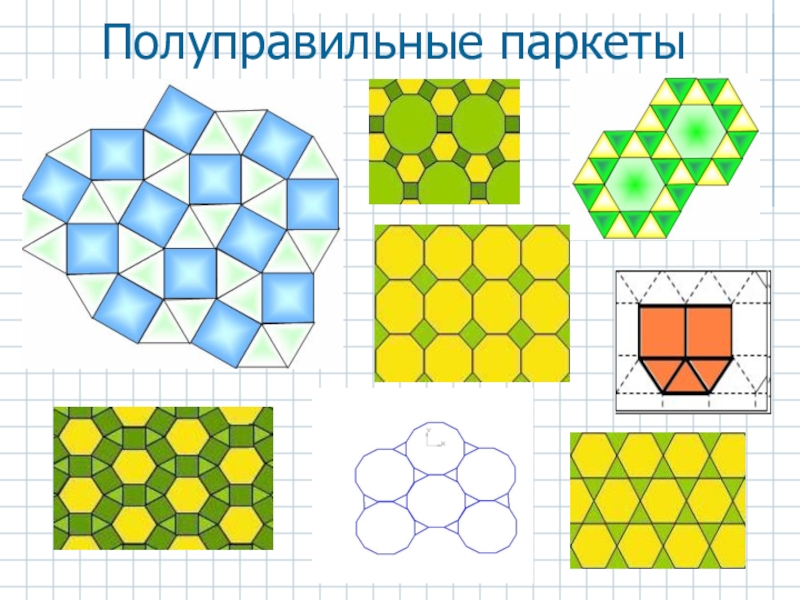
Слайд 8Полуправильные паркеты
Слайд 9Паркеты из неправильных многоугольников
Можно составить паркет из копий произвольного треугольника: из
двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма.
Легко покрыть плоскость параллелограммами

Слайд 10
Паркет, элементами которого являются одинаковые пятиугольники с углами 90°, 120°, 60°,
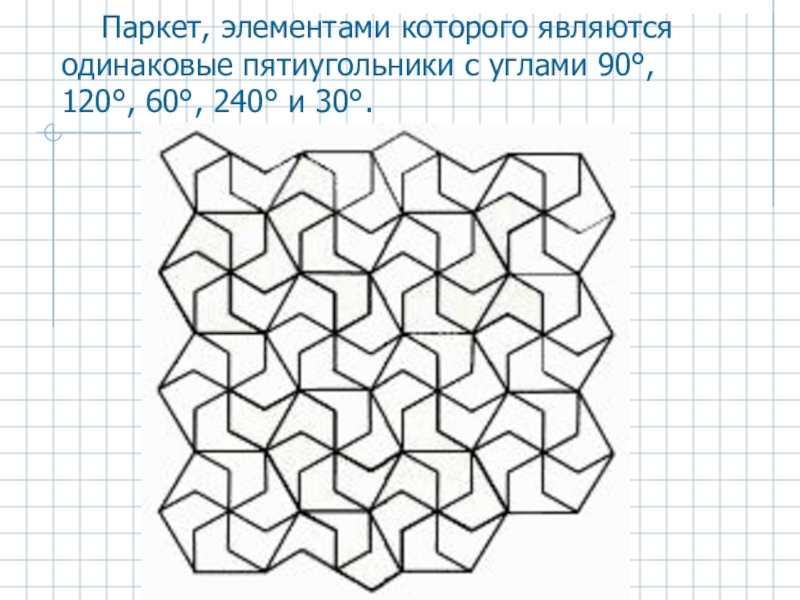
Слайд 11Паркеты из фигур, полученных комбинацией квадратов

Слайд 12 Паркеты Эшера
Обратимся к частным примерам из графического наследия голландского художника
Мориса Корнелиуса Эшера (1898-1972).

Слайд 13Правильные многоугольники в жизни

Слайд 14Паркеты в природе
Пчелы – удивительные творения природы. Геометрические способности пчел проявляются
при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета

Слайд 15
По результатам работы можно сделать следующие выводы:
— паркеты из правильных многоугольников
можно сделать только с помощью правильных треугольников, квадратов и правильных шестиугольников.
с помощью неправильных многоугольников можно придумать огромное количество паркетов.
в основе создания паркета лежит деление плоскости на многоугольники.
количество полуправильных паркетов конечно и равно 8.
из правильных: треугольника, квадрата и шестиугольника одинаковой площади наименьший периметр будет у шестиугольника.

Слайд 16Заключение
В результате изучения научной литературы о паркетах я подробно изучил паркеты,
понял принципы их построения, сделал вывод, что правильных паркетов одиннадцать, увидел их широкое применение в жизни людей.
В результате изучения данной темы я понял, что существует бесчисленное множество паркетов, но правильных только одиннадцать. Назначение своей работы я вижу в её использовании на занятиях, элективных курсах, уроках и внеклассных мероприятиях.
В процессе работы я узнал много нового, интересного. Данная тема дала мне возможность математического творчества.
Кроме того, полученные результаты довольно интересны и открывают широкие перспективы дальнейшего развития работы и применения полученных результатов.
Применение исследовательской работы:
Использование данной исследовательской работы в строительстве и ремонте жилых помещений, в украшении предметов пользования и т.д.
Источник: shareslide.ru
Презентация на тему Паркеты 9 класс
Что такое паркет ?Паркетом называют покрытие плоскости правильными многоугольниками, при которых два многоугольника либо имеют общую сторону, либо имеют общую вершину, либо совсем не имеют общих точек
Слайды и текст этой презентации
Слайд 1Паркеты
«Все вокруг – геометрия. Дух геометрического и математического порядка станет
властителем архитектурных судеб»
Ле Корбюзье

Слайд 2Что такое паркет ?
Паркетом называют покрытие плоскости правильными многоугольниками, при
которых два многоугольника либо имеют общую сторону, либо имеют общую
вершину, либо совсем не имеют общих точек

Слайд 3Что такое правильный паркет ?
Паркет называется правильным, если его можно
наложить на самого себя так, что любая заданная его вершина
наложится на другую заданную его вершину

Слайд 4Основная задача
Если длина стороны многоугольника
паркета задана , то существует только
конечное число различных
( не накладывающихся друг на друга ) правильных
Перечислить их все и тем самым ответить на вопрос об их числе — это и есть основная задача, которую нам предстоит решить

Слайд 5Некоторые указания

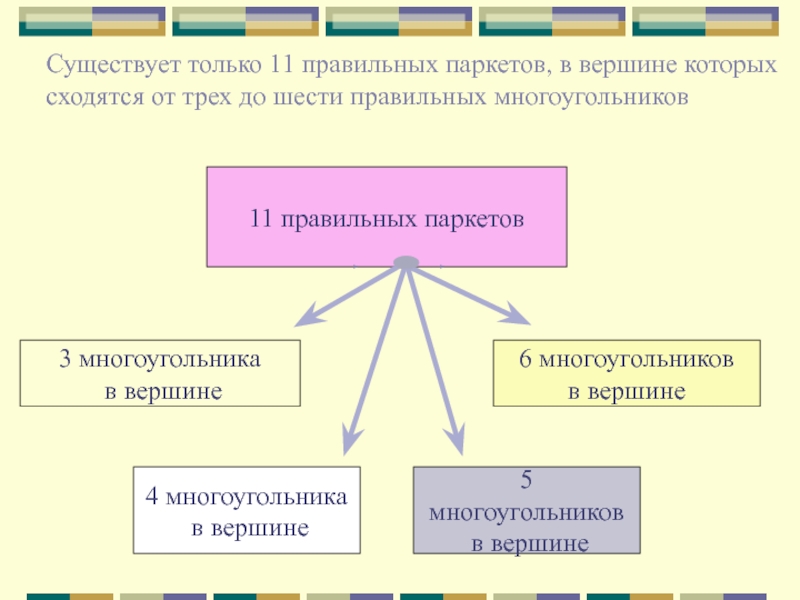
Слайд 63 многоугольника
в вершине
6 многоугольников
в вершине
4 многоугольника
в вершине
5 многоугольников
в вершине
Существует только 11 правильных паркетов, в вершине которых
сходятся
от трех до шести правильных многоугольников
11 правильных паркетов
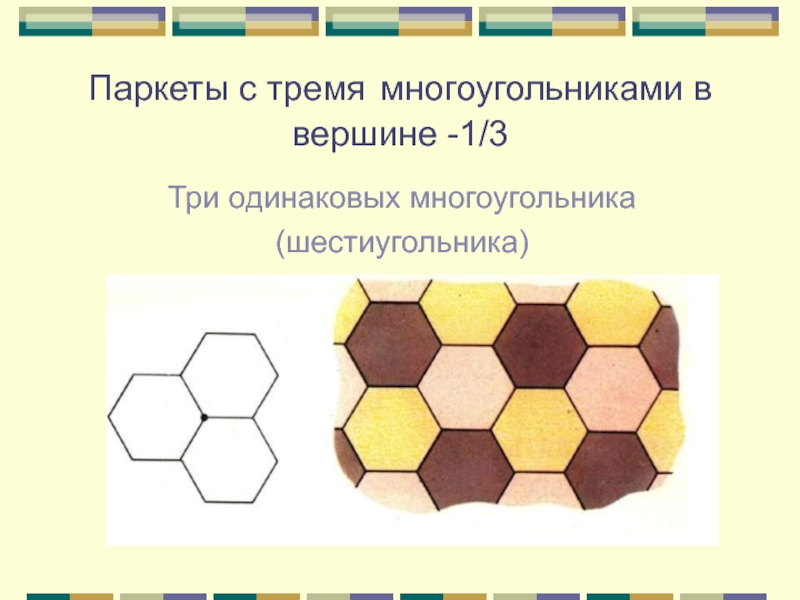
Слайд 7Паркеты с тремя многоугольниками в вершине -1/3
Три одинаковых многоугольника
(шестиугольника)
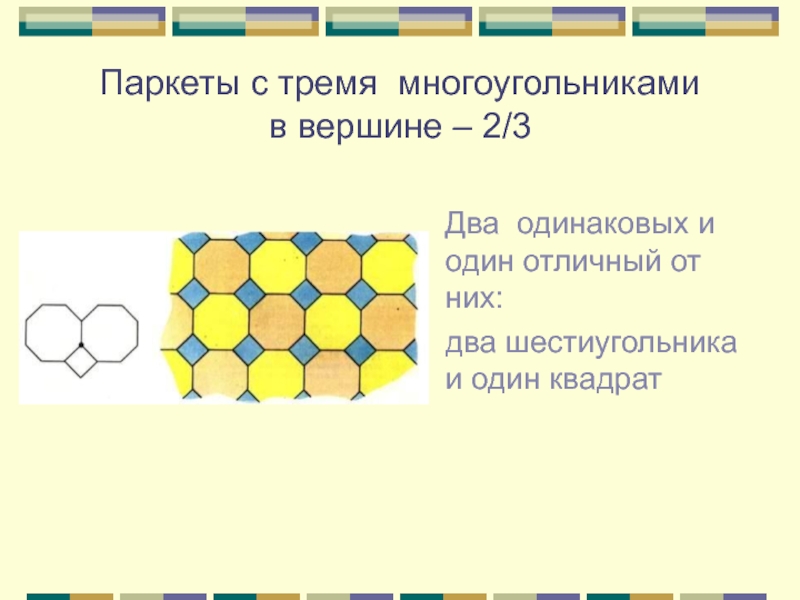
Слайд 8Паркеты с тремя многоугольниками в вершине – 2/3
Два одинаковых и
один отличный от них:
два шестиугольника и один квадрат
Слайд 9Паркеты с тремя многоугольниками в вершине– 3/3
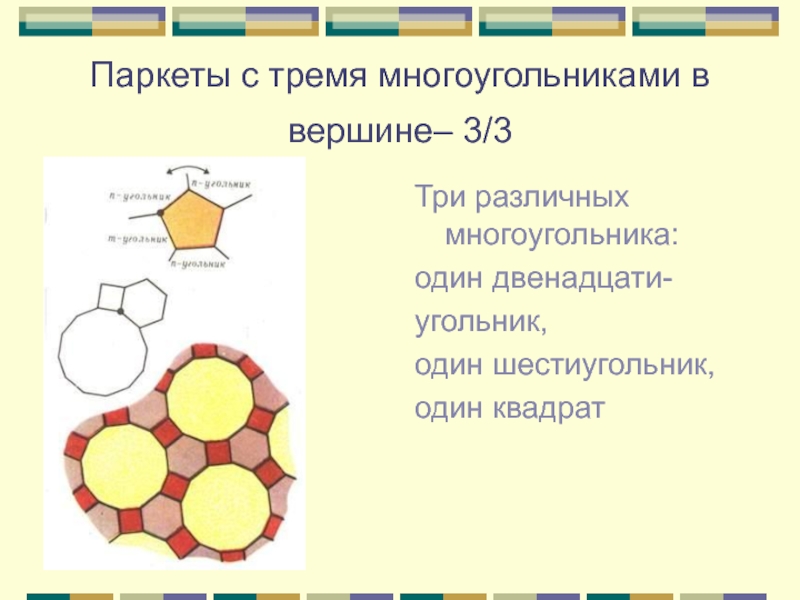
Три различных многоугольника:
один
двенадцати-
угольник,
один шестиугольник,
один квадрат
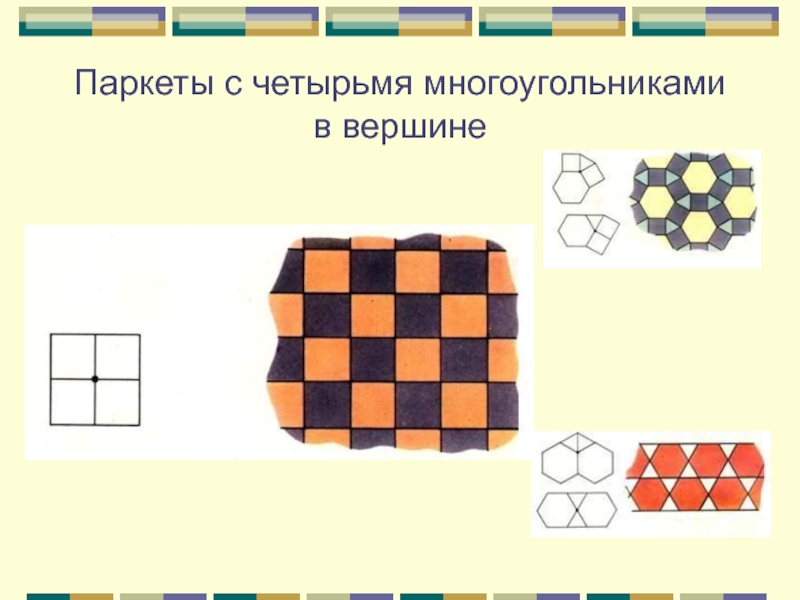
Слайд 10Паркеты с четырьмя многоугольниками в вершине
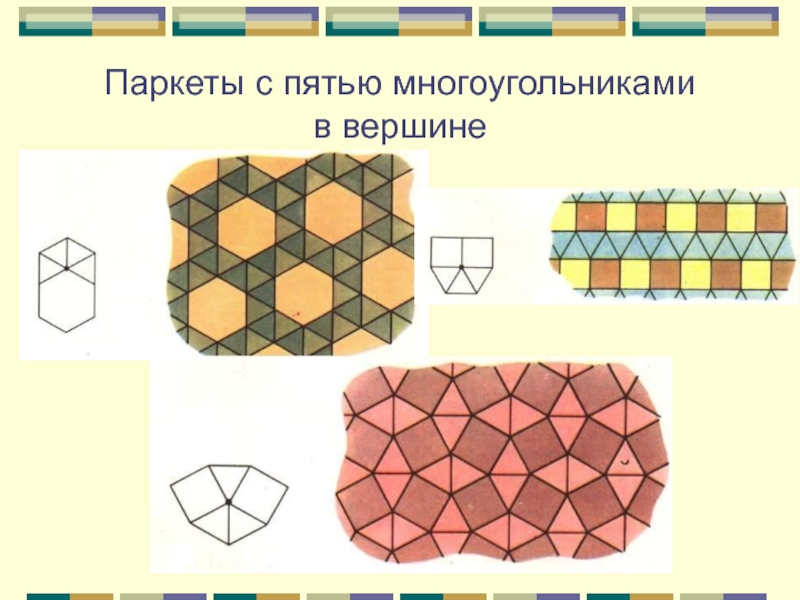
Слайд 11Паркеты с пятью многоугольниками в вершине
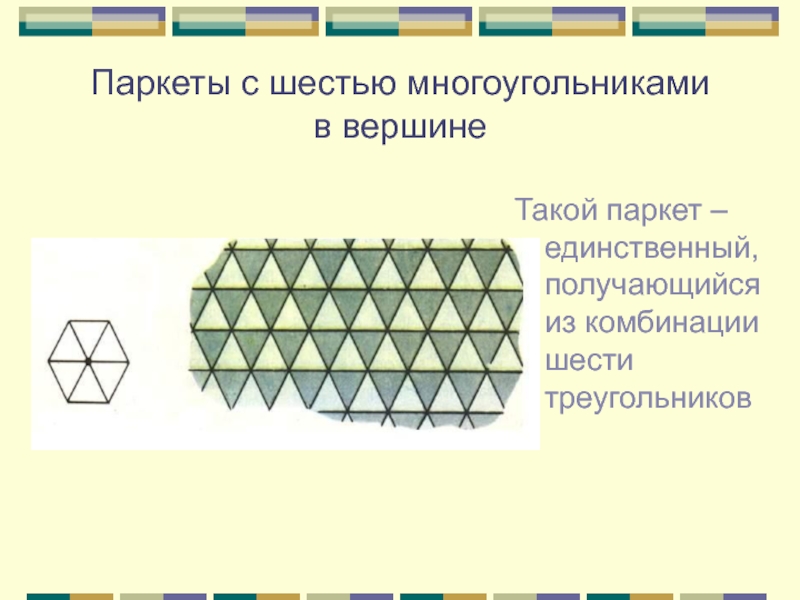
Слайд 12Паркеты с шестью многоугольниками в вершине
Такой паркет – единственный, получающийся из
комбинации шести треугольников
Слайд 13Паркеты из неправильных выпуклых четырехугольников
Олимпиадная задача:
Данным четырехугольником произвольной
формы настлать паркет, т.
е. заполнить всю
плоскость без пропусков и перекрытий.
Решается с помощью центральной
симметрии.
Отразим
четырехугольник симметрично
относительно середины одной из
сторон. Получим четырехугольник 2.
Теперь четырехугольник 2 отразим
симметрично относительно середины
другой стороны и т.д.
Такое построение можно провести
вокруг каждой вершины каждого из
новых четырехугольников, что и дает
паркет на всей плоскости.
Источник: theslide.ru